C++ Program to Check whether Graph is a Bipartite using BFS

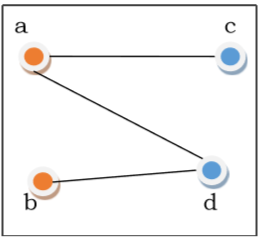
A bipartite graph is a graph in which if the graph coloring is possible using two colors i.e; vertices in a set are colored with the same color. This is a C++ program to Check whether a graph bipartite or not using BFS.

Algorithm

Begin
   Function Bipartite():
   1) Assign a color to the source vertex
   2) Color all the neighbors with another color except first one color.
   3) Color all neighbor’s neighbor with First color.
   4) Like this way, assign color to all vertices such that it satisfies all the constraints of k way coloring problem where k = 2.
   5) While assigning colors, if we find a neighbor which is colored with same color as current vertex, then the graph cannot be colored with 2 vertices i.e.; graph is not Bipartite
End

Example

#include <iostream>
#include <queue>
#define V 5
using namespace std;
bool Bipartite(int G[][V], int s) {
   int colorA[V];
   for (int i = 0; i < V; ++i)
   colorA[i] = -1;
   colorA[s] = 1; //Assign a color to the source vertex
   queue <int> q; //Create a queue of vertex numbers and enqueue source vertex for BFS traversal
   q.push(s);
   while (!q.empty()) {
      int w = q.front(); //dequeue a vertex
      q.pop();
      for (int v = 0; v < V; ++v) //Find all non-colored adjacent vertices {
         if (G[w][v] && colorA[v] == -1) //An edge from w to v exists and destination v is not colored {
            colorA[v] = 1 - colorA[w]; //Assign alternate color to this adjacent v of w
            q.push(v);
         } else if (G[w][v] && colorA[v] == colorA[w]) //An edge from w to v exists and destination
            //v is colored with same color as u
            return false;
      }
   }
   return true; //if all adjacent vertices can be colored with alternate color
}
int main() {
   int G[][V] = {{ 0, 1, 0, 0},
                { 1, 0, 0, 0},
                { 0, 0, 0, 1},
                { 1, 0, 1, 0}};
   if (Bipartite(G, 0))
      cout << "The Graph is Bipartite"<<endl;
   else
      cout << "The Graph is Not Bipartite"<<endl;
   return 0;
}

Output

The Graph is Bipartite

Paul Richard

Published on 26-Apr-2019 07:28:32

Previous Page Print Page