Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count the number of nodes at given level in a tree using BFS in C++
Given an undirected graph containing the nodes of a tree as vertices. The goal is to find the count of nodes at a given level of the tree using BFS( breadth first search ) algorithm.
BFS Algorithm:-
This algorithm starts traversing the graph/tree level by level. Starting from node at level 0, it will first traverse all nodes directly connected to it at level 1, then will traverse all nodes at next level and so on.
- Traverse nodes horizontally at current level.
- Traverse nodes at the next level in a similar manner.
Let us understand with examples.
For Example
Input - level=2
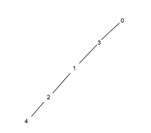
Output - Count of number of nodes at given level in a tree using BFS are: 1
Explanation - As shown above all levels have a single node in the graph.
Input - level=1
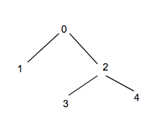
Output - Count of number of nodes at given level in a tree using BFS are: 2
Explanation - As shown above all levels have a single node in the graph. The nodes are 1, 2.
Approach used in the below program is as follows
In this approach we will traverse each node and set their levels as one level more than its parent. We will represent a graph using adjacency list representation.
If starting node is 0 then
level[0]=0,
level[1] = level[0]+1 = 1, level[2]=level[0]+1=1
level[3]= level[2]+1 = 2, level[4]=level[2]+1=2
- Create a class node representing a graph with data as number of vertices and next as pointer to adjacency list.
- Public method insert(int val, int point) adds edge to the graph.
- It adds val to point's adjacency list and point to val's adjacency list.
- Function count_nodes(int a, int b) returns the count of nodes at level b starting from source node a.
- Set the initial count as 0.
- Take bool array check = new bool[data].
- Array arr[data] stores the level of each vertex of the graph.
- Set all vertices of the graph as non-visited using for loop and set check[i] = false and arr[i] = 0.
- Create a queue l1 for BFS traversal.
- Mark started vertex visited as check[a] = true and add it to l1 using l1.push_back(a) and set its level as 0. arr[a] = 0.
- While the queue l1 is non-empty.
- Take the front element as a = l1. front() and print it using l1.pop_front().
- Mark all adjacent unvisited vertices of a as visited and add to queue l1.
- Set level of each adjacent vertex as level of a + 1.
- At the end of the while loop traverse arr[] using for loop and for each arr[i] == b increment count.
- At the end return count as result,
Example
#include <bits/stdc++.h>
using namespace std;
class node {
int data;
list < int > * next;
public:
node(int data) {
this -> data = data;
next = new list < int > [data];
}
void insert(int val, int point) {
next[val].push_back(point);
next[point].push_back(val);
}
int count_nodes(int a, int b);
};
int node::count_nodes(int a, int b) {
int count = 0;
bool * check = new bool[data];
int arr[data];
for (int i = 0; i < data; i++) {
check[i] = false;
arr[i] = 0;
}
list < int > l1;
check[a] = true;
l1.push_back(a);
arr[a] = 0;
while (!l1.empty()) {
a = l1.front();
l1.pop_front();
for (auto it = next[a].begin(); it != next[a].end(); ++it) {
if (!check[ * it]) {
arr[ * it] = arr[a] + 1;
check[ * it] = true;
l1.push_back( * it);
}
}
}
for (int i = 0; i < data; i++) {
if (arr[i] == b) {
count++;
}
}
return count;
}
int main() {
node n1(5);
n1.insert(1, 2);
n1.insert(0, 3);
n1.insert(1, 3);
n1.insert(2, 4);
int level = 1;
cout << "Count of number of nodes at given level in a tree using BFS are: " << n1.count_nodes(0, level);
return 0;
}If we run the above code it will generate the following output −
Output
Count of number of nodes at given level in a tree using BFS are: 1
926 Views
