
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count the nodes in the given tree whose sum of digits of weight is odd in C++
Given a binary tree with weights of its nodes. The goal is to find the number of nodes that have weights such that the sum of digits in that weights add up to an odd number. If weight is 12 then the digit sum is 3 which is odd so this node will be counted.
For Example
Input
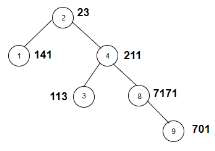
The tree which will be created after inputting the values is given below −
Output
Count of nodes in the given tree whose sum of digits of weight is odd are: 2
Explanation
we are given with the tree node and the weights associated with each node. Now we calculate the digit sum of each and every weight and check whether it's odd or not.
| Node | Weight | sum | ODD |
|---|---|---|---|
| 2 | 23 | 2+3=5 | yes |
| 1 | 141 | 1+4+1=6 | no |
| 4 | 211 | 2+1+1=4 | no |
| 3 | 133 | 1+1+3=5 | yes |
| 8 | 7171 | 7+1+7+1=16 | no |
| 9 | 101 | 7+0+1=8 | no |
Input
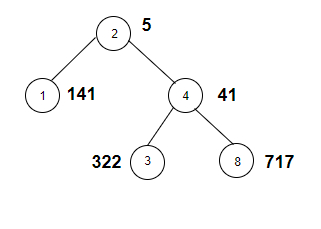
The tree which will be created after inputting the values is given below −
Output
Count of nodes in the given tree whose sum of digits of weight is odd are: 4
Explanation
we are given with the tree node and the weights associated with each node. Now we calculate the digit sum of each and every weight and check whether it's odd or not.
| Node | Weight | sum | ODD |
|---|---|---|---|
| 2 | 5 | 5 | yes |
| 1 | 141 | 1+4+1=6 | no |
| 4 | 41 | 4+1=4 | yes |
| 3 | 322 | 3+2+2=7 | yes |
| 8 | 717 | 7+1+7=15 | yes |
Approach used in the below program is as follows −
In this approach we will apply DFS on the graph of the tree to traverse it and check for the sum of digits of weight of each node, if it is odd. Take two vectors Node_Weight(100) and edge_graph[100] for this purpose.
Initialize Node_Weight[] with the weights of nodes.
Create a tree using vector edge_graph.
Take a global variable sum and initialize it with 0.
Function sum_total(int check) takes an integer and returns the sum of its digits.
Take initial sum as total=0.
Using a while loop calculate rightmost digits as check % 10 and add it to total. Reduce check by 10.
Return total as sum of digits of check.
Function odd_weight(int node, int root) takes a node and root node of a tree and returns the count of nodes in the given tree whose sum of digits of weight is odd.
Calculate total = sum_total(Node_Weight[node]) as sum of weight of node.
If total%2==1 its odd then increment sum.
If total%2==1 its odd then increment sum.
Call odd_weight(it, node) for the next node in the vector.
At the end of all functions we will have sum as number of nodes with weights having sum of digits as odd number.
Example
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int sum = 0;
int sum_total(int check){
int total = 0;
while(check){
total += check % 10;
check = check / 10;
}
return total;
}
void odd_weight(int node, int root){
int total = sum_total(Node_Weight[node]);
if (total % 2 == 1){
sum++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
odd_weight(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 23;
Node_Weight[1] = 141;
Node_Weight[4] = 211;
Node_Weight[3] = 115;
Node_Weight[8] = 7171;
Node_Weight[9] = 701;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
odd_weight(2, 2);
cout<<"Count the nodes in the given tree whose sum of digits of weight is odd are: "<<sum;
return 0;
}
Output
If we run the above code it will generate the following output −
Count the nodes in the given tree whose sum of digits of weight is odd are: 2

