Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Product of nodes at k-th level in a tree represented as string in C++
Given with the tree of nodes with data in a string format and the task is to find the product of the nodes at k-th level in a binary tree. Every node of a tree contains three things i.e. data part, left pointer for left subtree and right pointer for right subtree.
Level of binary tree starts from number 0 and it can go till ‘n’ which can be any positive number. So, we are given with the level ‘k’ and program must calculate the product of the nodes at given ‘k’ level.
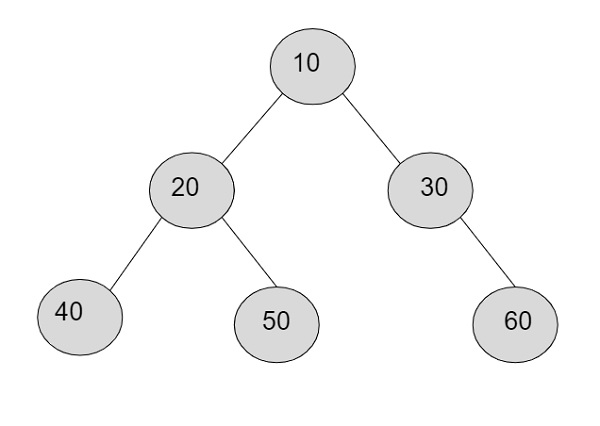
In the binary tree, if let’s say we are given with the value of k=2
So nodes at level 2 are − 40, 50, 60
Product= 40*50*60 = 1,20,000
Input
(1(2(3()())(4()(5()())))(6(7()())(8()()))) K = 1
Output
product of nodes at level k = 12
Input
(0(5(6()())(4()(9()())))(7(1()())(3()())))" k = 2
Output
product of nodes at level k = 72
Algorithm
Start
Step 1→ Declare function to calculate nodes at k-th level
int product(string tree, int k)
Declare int level = -1
Declare int product = 1
Declare int size = tree.length()
Loop For int i = 0 and i < size and i++
IF tree[i] = '('
Set level++
End
Else IF tree[i] = ')'
Set level—
End
Else
IF level = k
Set product *= (tree[i] - '0')
End
End
End
return product
Step 2→ In main()
Declare string tree = "(1(2(3()())(4()(5()())))(6(7()())(8()())))"
Declare int k = 1
Call product(tree, k)
StopExample
#include <bits/stdc++.h>
using namespace std;
//finding product at kth level
int product(string tree, int k){
int level = -1;
int product = 1;
int size = tree.length();
for (int i = 0; i < size; i++){
if (tree[i] == '(')
level++;
else if (tree[i] == ')')
level--;
else{
if (level == k)
product *= (tree[i] - '0');
}
}
return product;
}
int main(){
string tree = "(1(2(3()())(4()(5()())))(6(7()())(8()())))";
int k = 1;
cout <<"product of nodes at level k = "<<product(tree, k);
return 0;
}Output
If run the above code it will generate the following output −
product of nodes at level k = 12
Updated on: 13-Aug-2020
66 Views
Advertisements