Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count BST nodes that lie in a given range in C++
We are given a binary search tree made up of nodes and also a range and the task is to calculate the count of nodes that lies in the given range and display the result.
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −
The left subtree of a node has a key less than or equal to its parent node's key.
The right subtree of a node has a key greater than to its parent node's key.
Thus, BST divides all its sub-trees into two segments; the left subtree and the right subtree and can be defined as −
left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)
For Example
Input −
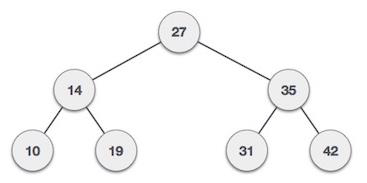
Range: [11, 40]
Output − count is: 5
Explanation − The node values between the range [11, 40] is 14, 19, 27, 31 and 35 so there are in total 5 nodes in a given binary search tree.
Approach used in the below program is as follows
Create a structure of a node containing data, left pointer, right pointer and create a range
Create a function to insert a newnode that the user will enter.
Create another function to count the nodes that lie in a given range.
Check IF the root is NULL then return
Now, check IF root->data = Start AND root->data = End then return 1.
Now, check IF root->data <= high && root->data >= low then return 1 + getCount(root->left, End, Start) + recursively_call_count_function(root->right, End, Start)
Else If, root->data < End then return recursively_call_count_function(root->right, End, Start)
Else, return recursively_call_count_function(root->left, End, Start)
Example
#include<iostream>
using namespace std;
// A BST node
struct node{
int data;
struct node* left, *right;
};
// Utility function to create new node
node *newNode(int data){
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return (temp);
}
int findcount(node *root, int low, int high){
// Base case
if (!root){
return 0;
}
if (root->data == high && root->data == low){
return 1;
}
// If current node is in range, then include it in count and
// recur for left and right children of it
if (root->data <= high && root->data >= low){
return 1 + findcount(root->left, low, high) +
findcount(root->right, low, high);
}
else if (root->data < low){
return findcount(root->right, low, high);
}
// Else recur for left child
else{
return findcount(root->left, low, high);
}
}
// main function
int main(){
// Let us construct the BST shown in the above figure
node *root = newNode(27);
root->left = newNode(14);
root->right = newNode(35);
root->left->left = newNode(10);
root->left->right = newNode(19);
root->right->left = newNode(31);
root->right->right = newNode(42);
int low = 10;
int high = 50;
cout << "Count of nodes between [" << low << ", " << high
<< "] is " << findcount(root, low, high);
return 0;
}Output
If we run the above code we will get the following output −
Count of nodes between [10, 50] is 7
165 Views
