Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum element between two nodes of BST in C++
Problem statement
Given an array of N elements and two integers A, B which belongs to the given array. Create a Binary Search Tree by inserting element from arr[0] to arr[n-1]. The task is to find the maximum element in the path from A to B.
Example
If array is {24, 23, 15, 36, 19, 41, 25, 35} the we can form BST as follows −
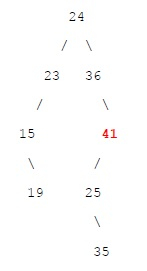
If we consider A = 19 and B = 41 then maximum element between these two nodes is 41
Algorithm
- Find Lowest Common Ancestor(LCA) of node A and B.
- Find maximum node between LCA and A. Let us call it as max1
- Find maximum node between LCA and B. Let us call it as max2
- Return maximum of max1 and max2
Example
Let us now see an example −
#include <bits/stdc++.h>
using namespace std;
struct node {
int data;
struct node* left;
struct node* right;
};
node *createNode(int x) {
node *p = new node();
p -> data = x;
p -> left = NULL;
p -> right = NULL;
return p;
}
void insertNode(struct node *root, int x) {
node *p = root, *q = NULL;
while (p != NULL) {
q = p;
if (p -> data < x) {
p = p -> right;
} else {
p = p -> left;
}
}
if (q == NULL) {
p = createNode(x);
} else {
if (q -> data < x) {
q -> right = createNode(x); } else {
q -> left = createNode(x);
}
}
}
int maxelpath(node *q, int x) {
node *p = q;
int mx = INT_MIN;
while (p -> data != x) {
if (p -> data > x) {
mx = max(mx, p -> data);
p = p -> left;
} else {
mx = max(mx, p -> data);
p = p -> right;
}
}
return max(mx, x);
}
int getMaximumElement(struct node *root, int x, int y) {
node *p = root;
while ((x < p -> data && y < p -> data) || (x > p ->
data && y > p -> data)) {
if (x < p -> data && y < p -> data) {
p = p -> left;
} else if (x > p -> data && y > p -> data) {
p = p -> right;
}
}
return max(maxelpath(p, x), maxelpath(p, y));
}
int main() {
int arr[] = {24, 23, 15, 36, 19, 41, 25, 35}; int a = 19, b = 41;
int n = sizeof(arr) / sizeof(arr[0]);
struct node *root = createNode(arr[0]);
for (int i = 1; i < n; i++) insertNode(root, arr[i]);
cout << "Maximum element = " << getMaximumElement(root, a, b) << endl;
return 0;
}Output
Maximum element = 41
Updated on: 31-Dec-2019
168 Views
Advertisements