Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count Balanced Binary Trees of Height h in C++
We are given with the height H of a binary tree. The goal is to find the number/count of balanced Binary Trees of given height.
A binary tree − is a tree data structure in which each node has at most two children, which are the left child and the right child.
Height-balanced binary tree − is defined as a binary tree in which the depth of the two subtrees of every node differ by 1 or 0 only. That is the height of the left subtree and the right subtree at every node has a maximum difference of 1.
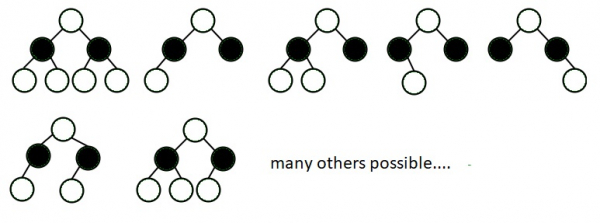
Following figure contains the possible height balanced binary trees for height h=3.
Input
Height H=2
Output
Count of Balanced Binary Trees of Height H is : 3
Explanation − Given figure contains possible balanced trees for height H=2
Input
Height H=3
Output
Count of Balanced Binary Trees of Height H is : 15
Approach used in the below program is as follows
The integer H is used to represent the height of Binary trees.
The function countBTheight(int h) takes the height of the tree as input and returns the number of possible Balanced Binary trees with height h.
We are using the recursive approach.
If the tree has height 1, i.e it has only one node then only one tree with a single node is present and that is balanced. ( if(h==1), return 1)
Otherwise the height is the sum of left and right subtrees with height one or two less than the root. (Balanced trees have a difference between the heights as 1).
The function returns the count as result.
Example
#include <iostream>
int countBTheight(int h){
// One tree is possible with height 0 or 1
if (h == 0 || h == 1)
return 1;
return countBTheight(h-1) * (2 *countBTheight(h-2) + countBTheight(h-1));
}
int main(){
int H = 4;
std::cout << "Count of balanced binary trees of height H is: "<<countBTheight(H);
}Output
Count of balanced binary trees of height H is: 315
286 Views
To Continue Learning Please Login