Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count the Number of Binary Search Trees present in a Binary Tree in C++
We are given a binary tree as input. The goal is to find the number of binary search trees (BSTs) present as subtrees inside it. A BST is a binary tree with left child less than root and right child more than the root.
For Example
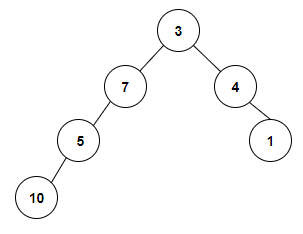
Input
The tree which will be created after inputting the values is given below −
Output
Count the Number of Binary Search Trees present in a Binary Tree are: 2
Explanation
we are given with an array of integer values that is used to form a binary tree and we will check whether there is a binary search tree present in it. Every root node represents the binary search tree so in the given binary tree we can see that there is no other binary search tree present therefore the count is 2 which is the total number of leaf nodes in a binary tree.
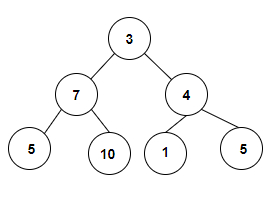
Input
The tree which will be created after inputting the values is given below −
Output
Count the Number of Binary Search Trees present in a Binary Tree are: 6
Explanation
we are given with an array of integer values that is used to form a binary tree and we will check whether there is a binary search tree present in it. Every root node represents the binary search tree so in the given binary tree we can see that there are 4 leaf nodes and two subtrees which are forming the BST therefore the count is 6.
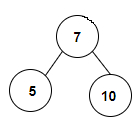
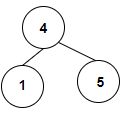
Approach used in the below program is as follows −
In this approach we will find the largest value of the node in the left subtree of node N and check if it is less than N. Also, we will find the smallest value in the right subtree of node N and check if it is more than N. If true, then it is a BST. Traverse the binary tree in bottom up manner and check above conditions and increment count of BSTs
The node of every node_data contains the information like number of BSTs present, maximum value in that tree, minimum value, boolean true if that subtree is a BST.
Function BST_present(struct tree_node* parent) finds the count of BSTs present inside the binary tree rooted at parent.
If the parent is NULL then return { 0, min, max, true } where min is INT-MIN and max is INT_MAX.
If left and right childs are null then return { 1, parent−>data, parent−>data, true }
Set node_data Left = BST_present(parent−>left); and node_data Right = BST_present(parent−>right);
Take node n1 and set n1.lowest = min(parent−>data, (min(Left.lowest, Right.lowest))) as lowest in its right subtree.
Set n1.highest = max(parent−>data, (max(Left.highest, Right.highest))); as highest in its left subtree.
if(Left.check && Right.check && parent−>data > Left.highest && parent−>data <Right.lowest) returns true then set n1.check = true as it is a BST.
Increase count of bsts as n1.total_bst = 1 + Left.total_bst + Right.total_bst;
Otherwise set n1.check = false and count as n1.total_bst = Left.total_bst + Right.total_bst.
At the end return n1.
Example
#include <bits/stdc++.h>
using namespace std;
struct tree_node{
struct tree_node* left;
struct tree_node* right;
int data;
tree_node(int data){
this−>data = data;
this−>left = NULL;
this−>right = NULL;
}
};
struct node_data{
int total_bst;
int highest, lowest;
bool check;
};
node_data BST_present(struct tree_node* parent){
if(parent == NULL){
int max = INT_MAX;
int min = INT_MIN;
return { 0, min, max, true };
}
if(parent−>left == NULL){
if(parent−>right == NULL){
return { 1, parent−>data, parent−>data, true };
}
}
node_data Left = BST_present(parent−>left);
node_data Right = BST_present(parent−>right);
node_data n1;
n1.lowest = min(parent−>data, (min(Left.lowest, Right.lowest)));
n1.highest = max(parent−>data, (max(Left.highest, Right.highest)));
if(Left.check && Right.check && parent−>data > Left.highest && parent−>data < Right.lowest){
n1.check = true;
n1.total_bst = 1 + Left.total_bst + Right.total_bst;
} else{
n1.check = false;
n1.total_bst = Left.total_bst + Right.total_bst;
}
return n1;
}
int main(){
struct tree_node* root = new tree_node(3);
root−>left = new tree_node(7);
root−>right = new tree_node(4);
root−>left−>left = new tree_node(5);
root−>right−>right = new tree_node(1);
root−>left−>left−>left = new tree_node(10);
cout<<"Count the Number of Binary Search Trees present in a Binary Tree are: "<<BST_present(root).total_bst;
return 0;
}Output
If we run the above code it will generate the following output −
Count the Number of Binary Search Trees present in a Binary Tree are: 2
1K+ Views
