Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Balanced Binary Tree in Python
In a binary tree, each node contains two children, i.e left child and right child. Let us suppose we have a binary tree and we need to check if the tree is balanced or not. A Binary tree is said to be balanced if the difference of height of left subtree and right subtree is less than or equal to '1'.
Example
Input-1:
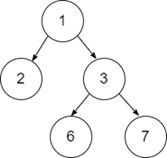
Output:
True
Explanation:
The given binary tree is [1,2,3, NULL, NULL, 6, 7]. The height difference of its left subtree and right subtree is equal to '1', thus it is a height Balanced tree.
Input-2:
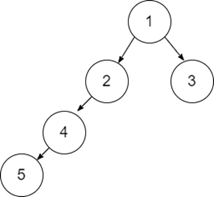
Output:
False
Explanation:
The given binary tree is [1,2,3,4, NULL, NULL,NULL,5]. The height difference of its left subtree and right subtree is greater than '1', thus it is not a height balanced tree.
Approach to Solve this Problem
The recursive approach to solve this problem is to find the height of the left subtree and the right subtree and then check if (height(leftsubstree) - height(rightsubtree) <= 1) and return True or False accordingly. Then, we will check recursively for each node of the binary tree.
- Take input of nodes of a Binary Tree.
- Define a function to find the height of the tree.
- A Boolean function to check recursively if the height difference of left subtree and right subtree is not more than '1', then return True.
- Return the Result.
Example
class treenode:
def __init__(self, data):
self.data = data
self.left = self.right = None
# funtion to find the height of the left subtree and right subtree
class height:
def __init__(self):
self.height = 0
# function to check if the tree is balanced or not
def isBalanced(root):
lh = height()
rh = height()
if root is None:
return True
return (
(abs(lh.height - rh.height) <= 1)
and isBalanced(root.left)
and isBalanced(root.right)
)
root = treenode(1)
root.left = treenode(2)
root.right = treenode(3)
root.left.left = None
root.left.right = None
root.right.left = treenode(6)
root.right.right = treenode(7)
if isBalanced(root):
print("Balanced")
else:
print("Not Balanced")Running the above code will generate the output as,
Output
Balanced
The given binary tree [1, 2, 3, NULL, NULL, 6, 7]. The height difference of its left subtree and right subtree is equal to '1', thus it is a height Balanced tree.
4K+ Views
