
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Unique Binary Search Trees in C++
The Unique Binary Search Trees problem is a classic dynamic programming problem that counts the number of unique binary search tree (BSTs) that can be formed with a given number of nodes. In this article, we will explain the problem, testcases, its solution, and provide a C++ implementation.
Number of Unique BSTs
In this problem, we are given an integer n, which represents the number of nodes in a binary search tree. The task is to find the number of different BSTs that can be formed using these n nodes and return the count. To understand the problem better, let's take a look at a few examples:
Scenario 1
Input: n = 3 Output: 5
Explanation: When we have 3 nodes, we can make following unique BSTs:
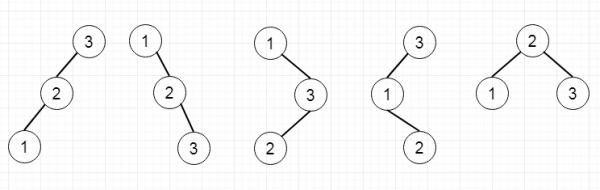
Scenario 2
Input: n = 1 Output: 1 Explanation: When we have 1 node, we can make only one unique BST.
Understanding the Problem
We have n distinct nodes labeled from 1 to n and we need to find the number of different BSTs that can be formed. First we need to understand properties of BSTs:
- For any node, the left subtree contains nodes smaller than the node.
- Similarly, the right subtree contains nodes greater than the node.
Now, if we choose a node i as the root, then left subtree can be formed using nodes from 1 to i-1 and right subtree can be formed using nodes from i+1 to n. With i as the root, we can form (i-1) * (n-i) unique BSTs. For large BSTs, first we need to find the number of unique BSTs that can be formed with smaller subtrees and then combine them. This indicates that we can use dynamic programming to solve this problem efficiently.
Example When n=3
Let's try all root choices: Root = 1 Left subtree: 0 nodes -> 1 BST (empty tree counts as 1 way) Right subtree: 2 nodes -> 2 BSTs Total for this root: 1 x 2 = 2 Root = 2 Left subtree: 1 node -> 1 BST Right subtree: 1 node -> 1 BST Total: 1 x 1 = 1 Root = 3 Left subtree: 2 nodes -> 2 BSTs Right subtree: 0 nodes -> 1 BST Total: 2 x 1 = 2 Finally, we can sum up the total unique BSTs for all root choices: Total unique BSTs = 2 + 1 + 2 = 5
DP Algorithm to Count Unique BSTs
To find unique BSTs for a given number, we can follow these steps:
- Initialize a DP array of size n+1 to store the number of unique BSTs for each count of nodes.
- Base case: There is 1 unique BST for 0 nodes (empty tree) and 1 unique BST for 1 node, so set dp[0] = 1 and dp[1] = 1.
- Iterate through the DP array from 2 to n.
- For each i, consider all possible roots from 1 to i.
- For each root j, the number of unique BSTs is the product of the number of unique BSTs in the left and right subtrees.
- Update the DP array with the total count for i nodes.
C++ Code to Count Unique BSTs
Here is the C++ implementation of the above algorithm:
#include <iostream>
#include <vector>
using namespace std;
int numTrees(int n) {
vector<long long> dp(n + 1, 0); // dp[i] = number of unique BSTs with i nodes
dp[0] = dp[1] = 1; // Base cases
for (int i = 2; i <= n; i++) {
for (int root = 1; root <= i; root++) {
dp[i] += dp[root - 1] * dp[i - root];
}
}
return dp[n];
}
int main() {
int n = 3;
cout << numTrees(n) << endl; // Output: 5
return 0;
}
The output of the above code will be:
5
Time Complexity and Space Complexity
The time complexity of this algorithm is O(n^2) because we have two nested loops: one for the number of nodes and another for the root choices.
The space complexity is O(n) due to the DP array used to store the number of unique BSTs for each count of nodes.

