
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
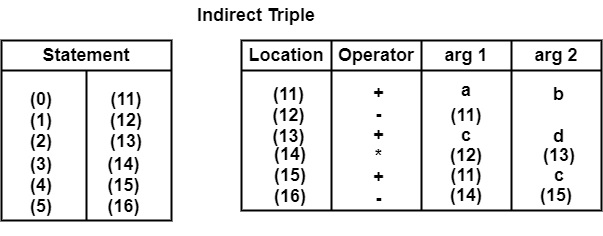
Construct Quadruples, Triples, and Indirect Triples for the expression\\n-(a + b) * (c + d) - (a + b + c)
Solution
First of all this statement will be converted into Three Address Code as−
t1 = a + b
t2 = −t1
t3 = c + d
t4 = t2 ∗ t3
t5 = t1 + c
t6 = t4 − t5
Quadruple
| Location | Operator | arg 1 | arg 2 | Result |
|---|---|---|---|---|
| (0) | + | a | b | t1 |
| (1) | − | t1 | t2 | |
| (2) | + | c | d | t3 |
| (3) | ∗ | t2 | t3 | t4 |
| (4) | + | t1 | c | t5 |
| (5) | − | t4 | t5 | t6 |
Triple
| Location | Operator | arg 1 | arg 2 |
| (0) | + | a | b |
| (1) | − | (0) | |
| (2) | + | c | d |
| (3) | ∗ | (1) | (2) |
| (4) | + | (0) | c |
| (5) | − | (3) | (4) |
Array Representation
Quadruple is a structure that contains atmost four fields, i.e., operator, Argument 1, Argument 2, and Result. The triples have three fields to represent the three address codes. The field of triples includes the name of the operator, the first source operand, and the second source operand.
This three address code representation contains three (3) fields, i.e., one for operator and two for arguments (i.e., Argument 1 and Argument 2). In this representation, temporary variables are not used. Instead of temporary variables, we use a number in parenthesis to represent a pointer to that particular record of the symbol table.
Quadruples & triples cause some wastage of memory because some fields are not occupied. To prevent wastage of space, the expression can be represented in a single array.
Example− Consider a statement
a = −b + c ∗ d
Its Three Address Code will be
t1 = −b
t2 = c ∗ d
t3 = t1 + t2
a = t3
Quadruples will be
| Location | Operator | arg 1 | arg 2 | Result |
| (0) | - | b | t1 | |
| (1) | * | c | d | t2 |
| (2) | + | t1 | t2 | t3 |
| (3) | = | t3 | A |
Since there is wastage of space in the Quadruple, so it can be converted into Array Representation as
| − | B | t1 | ∗ | C | d | t2 | + | t1 | t2 | t3 | = | t3 | a |
Advantage
It saves memory space.
Disadvantage
It cannot recognize a word, i.e., whether it is an operator or an operand. In Quadruple, it can be quickly done as operators & operands are written in their corresponding fields.

