Check if a given Binary Tree is height balanced like a Red-Black Tree in Python

Suppose there is a Red-Black Tree, here the largest height of a node is at most double the minimum height. If we have a binary search tree, we have to check the following property. With respect of every node, length of the longest leaf to node path has not more than double the nodes on shortest path from node to leaf.

So, if the input is like

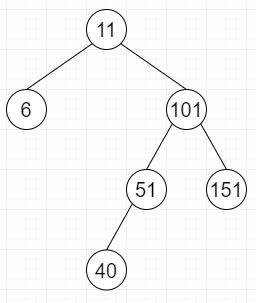
then the output will be True, as this is balanced.

To solve this, we will follow these steps −

• Define a function solve() . This will take root, max_height, min_height
• if root is null, then
  • max_height := 0, min_height := 0
  • return True
• left_max := 0, left_min := 0
• right_max := 0, right_min := 0
• if solve(root.left, left_max, left_min) is same as False, then
  • return False
• if solve(root.right, right_max, right_min) is same as False, then
  • return False
• max_height := maximum of left_max and right_max + 1
• min_height := minimum of left_min and right_min + 1
• if max_height <= 2 * min_height, then
  • return True
• return False
• From the main method do the following −
• max_height := 0, min_height := 0
• return solve(root, max_height, min_height)

Example

Let us see the following implementation to get better understanding −

 Live Demo

class TreeNode:
   def __init__(self, key):
      self.data = key
      self.left = None
      self.right = None
def solve(root, max_height, min_height) :
   if (root == None) :
      max_height = min_height = 0
      return True
   left_max=0
   left_min=0
   right_max, right_min=0,0
   if (solve(root.left, left_max, left_min) == False) :
      return False
   if (solve(root.right, right_max, right_min) == False) :
      return False
   max_height = max(left_max, right_max) + 1
   min_height = min(left_min, right_min) + 1
   if (max_height <= 2 * min_height) :
      return True
   return False
def is_tree_balanced(root) :
   max_height, min_height = 0,0
   return solve(root, max_height, min_height)
root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(100)
root.right.left = TreeNode(50)
root.right.right = TreeNode(150)
root.right.left.left = TreeNode(40)
print(is_tree_balanced(root))

Input

root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(100)
root.right.left = TreeNode(50)
root.right.right = TreeNode(150)
root.right.left.left = TreeNode(40)

Output

True

Arnab Chakraborty

Published on 27-Aug-2020 13:08:22

• Related Questions & Answers
• Check if a given Binary Tree is height balanced like a Red-Black Tree in C++
• Check if a given Binary Tree is Heap in Python
• Balanced Binary Tree in Python
• Check if a given Binary Tree is SumTree in C++
• Check if a given Binary Tree is Heap in C++
• Check if a binary tree is subtree of another binary tree in C++
• Program to check whether a tree is height balanced or not in C++
• C++ program to Check if a Given Binary Tree is an AVL Tree or Not
• C++ Program to Check Whether a Given Tree is Binary Search Tree
• C++ Program to Check Whether a given Binary Tree is a Full Binary Tree or not
• Insertion in the Red Black Tree in Data Structure
• Check if a given graph is tree or not
• C++ Program to Check if a Binary Tree is a BST
• Check if a binary tree is sorted levelwise or not in C++
• Program to find out if a BST is present in a given binary tree in Python