
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Bijective Function in Automata Theory
A bijective function, also known as a bijection, is a function that is both one-to-one (injective) and onto (surjective). These concepts are important in mathematics, particularly in set theory and other branches that involve functions. We will see the basic definitions, provide examples, and explain the criteria for a function to be bijective for a better understanding.
What is a Bijective Function?
A bijective function is a function that satisfies two main criteria −
- One-to-One (Injective) − Every element in the domain (Set A) maps to a distinct element in the codomain (Set B).
- Onto (Surjective) − Every element in the codomain (Set B) is mapped by at least one element in the domain (Set A).
If a function meets both these criteria, it is called a bijection.
Formally we can say, a function f from Set A to Set B is bijective if it is both one to one and onto. This means that each element in Set A maps to a unique element in Set B, and every element in Set B has a corresponding element in Set A.
In simpler terms, in a bijective function, there is a perfect pairing between the elements of Set A and Set B.
Understanding One-to-One (Injective) Function
Let us recap the one-to-one function which is needed for bijective functions.
One-to-One Mapping
A function is one-to-one if each element in the domain (Set A) has a unique image in the codomain (Set B). In other words, no two different elements in Set A map to the same element in Set B.
For example −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3\}}$$
$$\mathrm{Set \:B \:=\: \{a,\: b,\: c,\: d\}}$$
If we map 1 to a, 2 to b, and 3 to c, the function is one-to-one because each element in Set A has a distinct image in Set B.
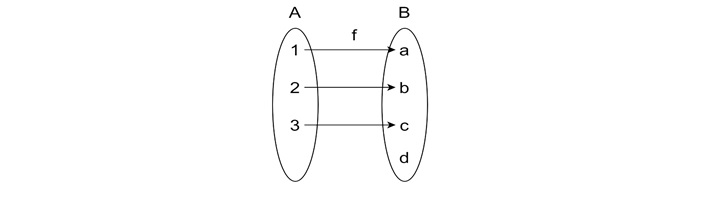
Example of Non-One-to-One Mapping
Suppose Set A has four elements {1, 2, 3, 4} and Set B has three elements {a, b, c}, and we map as shown in the figure below. This function is not one-to-one because two different elements in Set A (3 and 4) map to the same element in Set B (C).
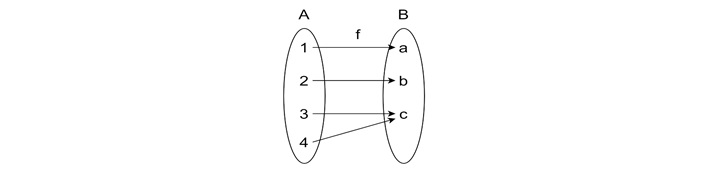
The key takeaway idea is that for a function to be one to one, the number of elements in Set A must be less than or equal to the number of elements in Set B.
Understanding Surjective (Onto) Function
Let's recap the concept of onto functions.
Onto Mapping
A function is onto if every element in the codomain (Set B) is mapped by at least one element in the domain (Set A). In an onto function, no element in Set B is left unmapped.
For example −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3,\: 4\}}$$
$$\mathrm{Set \:B \:=\: \{a,\: b,\: c\}}$$
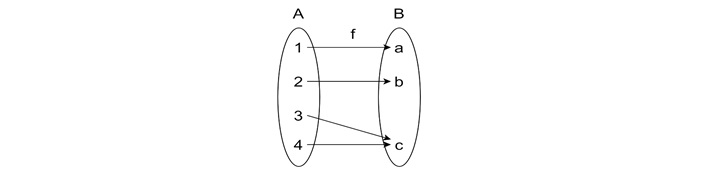
Example of Non-Onto Mapping
If $\mathrm{Set \:A \:=\: \{1,\: 2,\: 3\}}$ and $\mathrm{Set \:B \:=\: \{a,\: b,\: c,\: d\}}$, and we map −
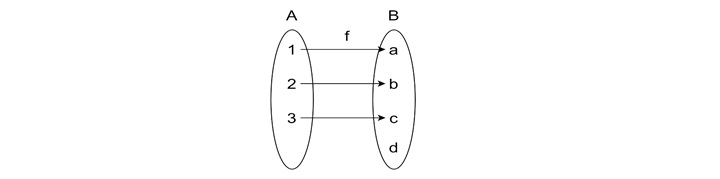
Element d in Set B is left unmapped, so the function is not onto.
The criterion for a function to be onto is that the number of elements in Set A should be greater than or equal to the number of elements in Set B. If Set A has fewer elements than Set B, the function cannot be onto.
Combining One-to-One and Onto: The Bijective Function
A function is bijective if it is both one-to-one and onto. For a function to be bijective, the number of elements in Set A must be equal to the number of elements in Set B.
Example of a Bijective Function
Let's consider an example where Set A and Set B have the same number of elements −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3,\: 4\}}$$
$$\mathrm{Set \:B \:=\: \{a,\: b,\: c,\: d\}}$$
We can map −

This function is both one-to-one (each element in Set A has a distinct image) and onto (each element in Set B has a pre-image). Therefore, it is a bijection.
Example of Non-Bijective Function
Consider the function −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3,\: 4\}}$$
$$\mathrm{Set \:B \:=\: \{A,\: B,\: C\}}$$
If we map −
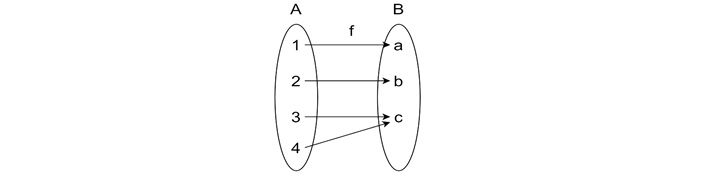
This function is neither one-to-one (because 3 and 4 map to the same element in Set B) nor onto (because not all elements in Set B have pre-images). Therefore, it is not a bijection.
Bijective Function with Infinite Sets
The concept of bijective functions becomes more useful when used in infinite sets. For finite sets, if Set A and Set B have the same number of elements, and the function is one-to-one, it is also onto, making it bijective. However, this is not always the case with infinite sets.
Example of Bijective Function with Infinite Sets
Let us consider a function from the set of natural numbers to itself −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3,\: \dotso\}}$$
$$\mathrm{Set \:B \:=\: \{1,\: 2,\: 3,\: \dotso\}}$$

If we define the function f(x) = x, where each natural number maps to itself, the function is both one-to-one and onto. Therefore, it is a bijection.
Example of Non-Bijective Function with Infinite Sets
Now, consider a different function −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3,\: \dotso\}}$$
$$\mathrm{Set \:B \:=\: \{1,\: 2,\: 3,\: \dotso\}}$$
If we define the function f(x) = 2x, where −
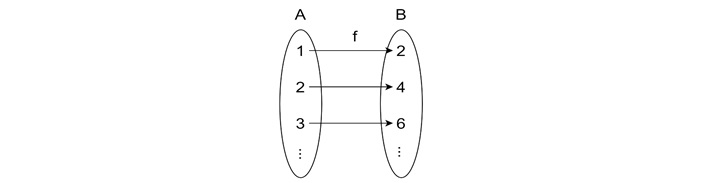
This function is one-to-one, but not onto because odd numbers in Set B have no pre-images in Set A. Therefore, it is not a bijection.
Counting the Number of Bijective Function
The number of bijective functions between two finite sets with the same number of elements can be calculated using factorials.
Example: Calculating Number of Bijections
If Set A and Set B both have n elements, then the number of bijective functions is n! (n factorial).
For example, if −
$$\mathrm{Set \:A \:=\: \{1,\: 2,\: 3\}}$$
$$\mathrm{Set \:B \:=\: \{A,\: B,\: C\}}$$
The number of bijective functions is −
$$\mathrm{3! \:=\: 3 \:\times\: 2 \:\times\: 1 \:=\: 6}$$
It means, there are six possible bijections between these two sets.
Conclusion
In this chapter, we explained the concept of bijective functions. We discussed examples of both bijective and non-bijective functions, including cases with finite and infinite sets. We also learned how to calculate the number of bijective functions between two finite sets.