
- PHP - Home
- PHP - Roadmap
- PHP - Introduction
- PHP - Installation
- PHP - History
- PHP - Features
- PHP - Syntax
- PHP - Hello World
- PHP - Comments
- PHP - Variables
- PHP - Echo/Print
- PHP - var_dump
- PHP - $ and $$ Variables
- PHP - Constants
- PHP - Magic Constants
- PHP - Data Types
- PHP - Type Casting
- PHP - Type Juggling
- PHP - Strings
- PHP - Boolean
- PHP - Integers
- PHP - Files & I/O
- PHP - Maths Functions
- PHP - Heredoc & Nowdoc
- PHP - Compound Types
- PHP - File Include
- PHP - Date & Time
- PHP - Scalar Type Declarations
- PHP - Return Type Declarations
- PHP - Operators
- PHP - Arithmetic Operators
- PHP - Comparison Operators
- PHP - Logical Operators
- PHP - Assignment Operators
- PHP - String Operators
- PHP - Array Operators
- PHP - Conditional Operators
- PHP - Spread Operator
- PHP - Null Coalescing Operator
- PHP - Spaceship Operator
- PHP Control Statements
- PHP - Decision Making
- PHP - If…Else Statement
- PHP - Switch Statement
- PHP - Loop Types
- PHP - For Loop
- PHP - Foreach Loop
- PHP - While Loop
- PHP - Do…While Loop
- PHP - Break Statement
- PHP - Continue Statement
- PHP Arrays
- PHP - Arrays
- PHP - Indexed Array
- PHP - Associative Array
- PHP - Multidimensional Array
- PHP - Array Functions
- PHP - Constant Arrays
- PHP Functions
- PHP - Functions
- PHP - Function Parameters
- PHP - Call by value
- PHP - Call by Reference
- PHP - Default Arguments
- PHP - Named Arguments
- PHP - Variable Arguments
- PHP - Returning Values
- PHP - Passing Functions
- PHP - Recursive Functions
- PHP - Type Hints
- PHP - Variable Scope
- PHP - Strict Typing
- PHP - Anonymous Functions
- PHP - Arrow Functions
- PHP - Variable Functions
- PHP - Local Variables
- PHP - Global Variables
- PHP Superglobals
- PHP - Superglobals
- PHP - $GLOBALS
- PHP - $_SERVER
- PHP - $_REQUEST
- PHP - $_POST
- PHP - $_GET
- PHP - $_FILES
- PHP - $_ENV
- PHP - $_COOKIE
- PHP - $_SESSION
- PHP File Handling
- PHP - File Handling
- PHP - Open File
- PHP - Read File
- PHP - Write File
- PHP - File Existence
- PHP - Download File
- PHP - Copy File
- PHP - Append File
- PHP - Delete File
- PHP - Handle CSV File
- PHP - File Permissions
- PHP - Create Directory
- PHP - Listing Files
- Object Oriented PHP
- PHP - Object Oriented Programming
- PHP - Classes and Objects
- PHP - Constructor and Destructor
- PHP - Access Modifiers
- PHP - Inheritance
- PHP - Class Constants
- PHP - Abstract Classes
- PHP - Interfaces
- PHP - Traits
- PHP - Static Methods
- PHP - Static Properties
- PHP - Namespaces
- PHP - Object Iteration
- PHP - Encapsulation
- PHP - Final Keyword
- PHP - Overloading
- PHP - Cloning Objects
- PHP - Anonymous Classes
- PHP Web Development
- PHP - Web Concepts
- PHP - Form Handling
- PHP - Form Validation
- PHP - Form Email/URL
- PHP - Complete Form
- PHP - File Inclusion
- PHP - GET & POST
- PHP - File Uploading
- PHP - Cookies
- PHP - Sessions
- PHP - Session Options
- PHP - Sending Emails
- PHP - Sanitize Input
- PHP - Post-Redirect-Get (PRG)
- PHP - Flash Messages
- PHP AJAX
- PHP - AJAX Introduction
- PHP - AJAX Search
- PHP - AJAX XML Parser
- PHP - AJAX Auto Complete Search
- PHP - AJAX RSS Feed Example
- PHP XML
- PHP - XML Introduction
- PHP - Simple XML Parser
- PHP - SAX Parser Example
- PHP - DOM Parser Example
- PHP Login Example
- PHP - Login Example
- PHP - Facebook Login
- PHP - Paypal Integration
- PHP - MySQL Login
- PHP Advanced
- PHP - MySQL
- PHP.INI File Configuration
- PHP - Array Destructuring
- PHP - Coding Standard
- PHP - Regular Expression
- PHP - Error Handling
- PHP - Try…Catch
- PHP - Bugs Debugging
- PHP - For C Developers
- PHP - For PERL Developers
- PHP - Frameworks
- PHP - Core PHP vs Frame Works
- PHP - Design Patterns
- PHP - Filters
- PHP - JSON
- PHP - Exceptions
- PHP - Special Types
- PHP - Hashing
- PHP - Encryption
- PHP - is_null() Function
- PHP - System Calls
- PHP - HTTP Authentication
- PHP - Swapping Variables
- PHP - Closure::call()
- PHP - Filtered unserialize()
- PHP - IntlChar
- PHP - CSPRNG
- PHP - Expectations
- PHP - Use Statement
- PHP - Integer Division
- PHP - Deprecated Features
- PHP - Removed Extensions & SAPIs
- PHP - PEAR
- PHP - CSRF
- PHP - FastCGI Process
- PHP - PDO Extension
- PHP - Built-In Functions
PHP - Recursive Functions
A recursive function is such a function that calls itself until a certain condition is satisfied. In PHP, it is possible to defines a recursive function.
Recursion is used when a certain problem is defined in terms of itself.
Sometimes, it can be tedious to solve a problem using iterative approach. Recursive approach provides a very concise solution to seemingly complex problems.
Recursion in PHP is very similar to the one in C and C++.
Recursive functions are particularly used in traversing nested data structures, and searching or sorting algorithms.
Binary tree traversal, heap sort and finding shortest route are some of the cases where recursion is used.
Calculation of Factorial using Recursion
The most popular example of recursion is calculation of factorial. Mathematically factorial is defined as −
n! = n (n-1)!
It can be seen that we use factorial itself to define factorial. Hence, this is a fit case to write a recursive function.
Let us expand the above definition for calculation of factorial value of 5
5! = 5 4!
5 4 3!
5 4 3 2!
5 4 3 2 1!
5 4 3 2 1
= 120
While we can perform this calculation using a loop, its recursive function involves successively calling it by decrementing the number till it reaches 1.
Example
Following is the recursive function to calculate factorial.
<?php
function factorial ($n) {
if ($n == 1) {
echo $n . PHP_EOL;
return 1;
} else {
echo "$n * ";
return $n*factorial($n-1);
}
}
echo "Factorial of 5 = " . factorial(5);
?>
Output
It will produce the following output −
5 * 4 * 3 * 2 * 1 Factorial of 5 = 120
Binary Search using Recursion
Let us have a look at another example to understand how recursion works. The problem at hand is to check whether a given number is present in a list.
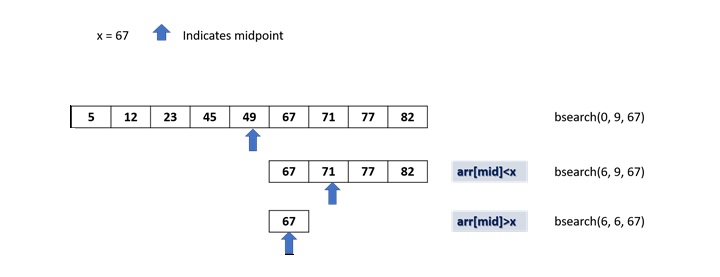
While we can perform a sequential search for a certain number in the list using a for loop and comparing each number, the sequential search is not efficient especially if the list is too large. Here, we can use the binary search algorithm that checks if the index 'high' is greater than index 'low. Based on the value present at 'mid' variable, the function is called again to search for the element.
We have a list of numbers, arranged in ascending order. Then, we find the midpoint of the list and restrict the checking to either left or right of midpoint depending on whether the desired number is less than or greater than the number at midpoint.
The following diagram shows how binary search works −
Example
The following code implements the recursive binary searching technique −
<?php
function bsearch($my_list, $low, $high, $elem) {
if ($high >= $low) {
$mid = intval(($high + $low)/2);
if ($my_list[$mid] == $elem)
return $mid;
elseif ($my_list[$mid] > $elem)
return bsearch($my_list, $low, $mid - 1, $elem);
else
return bsearch($my_list, $mid + 1, $high, $elem);
}
else
return -1;
}
$list = [5,12,23, 45, 49, 67, 71, 77, 82];
$num = 67;
$result = bsearch($list,0,count($list)-1, $num);
if ($result != -1)
echo " Number $num found at index " . $result;
else
echo "Element not found!";
?>
Output
It will produce the following output −
Number 67 found at index 5
You can check the output for different numbers present in the given list, as well as those which are not present in the list.