Modulus Function

Introduction

• A modulus function can be used to find the magnitude of a number irrespective of its sign.

• In other words, a modulus function gives the magnitude of a number.

• A modulus function also determines the distance of a number from the origin.

• It always gives the non-negative value of the function.

• It is used in almost all the major scientific measurements.

• Modulus functions are represented as a=|x|.

• In this tutorial, we are going to learn about the functions, absolute(modulus) fFunction, graph of absolute function, properties of absolute function, rules of definite integration of absolute function, continuity and differentiability of absolute functions, signum function, and some solved example to help us better understand the concept.

Functions

• Functions are special types of relations between variables and numbers.

• Functions can be referred to as a set of rules which produces new outputs out of given elements.

• Consider set A and set B with relation If $\mathit{f}$, it is said to be a function if elements of set A have their image in set B.

• If $\mathit{f}$ is a function from set A to set B and $\mathrm{(a,b) \in \mathit{f}, then\: \mathit{f}(a) = b.}$

Absolute (Modulus) Function

• As we know, modulus function gives the absolute value of a function irrespective of their sign. The value of the modulus function is always greater than or equal to zero. It is denoted as f(x) = |x|,where f: R → (0,∞) and x ∈ R.

• For a real number “x”, |x| is the modulus of x. If x is a non-zero real number greater than zero, f(x) gives the absolute value of x.

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

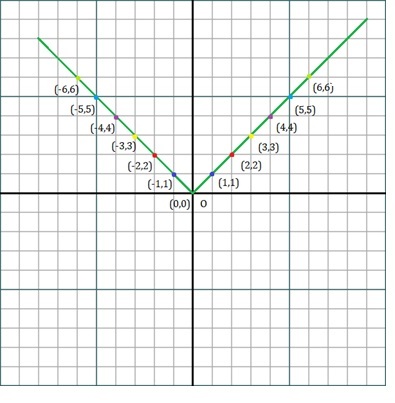
Graph of Absolute function

For a variable “x”, taking values from -6 to 6, finding the modulus for the positive values and negative values of 'x', we plot the graph as 'y = x' and 'y = -x'.

X	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
f(x)=x	6	5	4	3	2	1	0	1	2	3	4	5	6

Plotting it against the graph.

Properties of Absolute Function

Following are the properties of modulus function which can help us better understand their application.

• Property 1 − The modulus function gives the absolute value as output for all real values of x. Therefore, there can always be a positive value for modulus function.

|x| = p; if p is greater than 0, then x = ± p ;

|x| = p; if p is equal to 0, then x = 0 ;

If |x| = p, x cannot be zero.

• Property 2 −

  • Case1:If p is greater than 0

    |f(x)| < p and p > 0 ⇒ -p < f(x) < p

    |f(x)| > p and p > 0 ⇒ -p < f(x) (or) f(x) > p

  • Case2: If p is less than 0

    |f(x)| < p and p < 0; there cannot be any solution.

    |f(x)| > p and p < 0; allowed for all real values of f(x).

• Property 3 − If p, q belong to real numbers, then

  $$\mathrm{|-p| = |p|}$$

  $$\mathrm{|p-q| = 0 \Leftrightarrow p=q}$$

  $$\mathrm{|p+q| \leq |p| + |q|}$$

  $$\mathrm{|p-q| \geq ||p| - |q||}$$

  $$\mathrm{|pq| = |p| |q|}$$

  |p/q| = |p|/|q|, q not equal to zero.

Rules of Definite Integration of Absolute Function

Rule 1 − For evaluating the definite integral of modulus function, we find the x intercept by equating the given function to zero.

Rule 2 − The shape of the graph drawn for a modulus function will always be a “V”.

Rule 3 − By putting the given intervals, we divide the integral into parts and integrate.

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

The integral of modulus function can be written as:

$$\mathrm{\int \mathit{f}(x)=(\frac{1}{2})x^2+C \:\:\:\:\:\:\: x≥0}$$

$$\mathrm{\int \mathit{f}(x)=-(\frac{1}{2})x^2+C \:\:\:\:\:\:\: x<0}$$

Continuity and Differentiability of Absolute Functions

Absolute continuity allows us to obtain the continuity of the modulus functions. For example −

For a modulus function |x+3|+|x-2|, to find the continuity we split it into two functions −

|x+3| and |x-2|

x=-3 and x=2

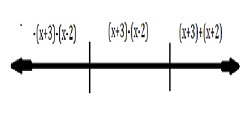
f(x)=-x-3-x+2=-2x-1 If x<-3

f(x)=x+3-x+2=5 if -3<x<2

f(x)=x+3+x-2=2x+1 if x≥2

Now let's learn the differentiability of absolute functions.

We know that the f(x)=|x| equals x, if x>0, and -x if x<0

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

Therefore, the derivative of the modulus function f(x)=|x| equals 1 if x>0, and -1 if <0

$$\mathrm{\frac{d\{f(x)\}}{dx}=1,if\: x>0}$$

$$\mathrm{\frac{d\{f(x)\}}{dx}=-1,if\: x<0}$$

Derivative of modulus function: $\mathrm{\frac{d\{|x|\}}{dx}=\frac{x}{\{|x|\}}}$, for all the values of x other than zero.

Signum Function

The Signum function can be defined by the following

$$\mathrm{f(x)=1,if\: x>0}$$

$$\mathrm{f(x)=0,if\: x=0}$$

$$\mathrm{f(x)=-1,if\: x <0}$$

Where x is a real number, and the range is {-1,0,1}

Solved Examples

1.Find the value of the modulus function |x| for x = -2 and x = 5.

Solution:

If x=-2, then |x| = |-2| =2

If x = 5, then |x| = |5| = 5

Answer:

|x| = 2 for x = -2 and |x| = 5 for x = 5

2.Find the modulus for the function |x + 5| = 10.

Solution:

The value of the modulus function is non-negative, following cases arise −

If x + 5> 0, then the modulus |x + 5| = x + 5, and if x + 5 < 0, then |x + 5| = -(x +5).

Case 1 − If x + 5> 0, then

|x + 5| = x + 5

⇒ x + 5 = 10

⇒ x = 10-5 = 5

Case 2 − If x +5 < 0, then

⇒ -(x + 5) = 10

⇒ -x - 5 = 10

⇒ x = -5 - 10 = -15

Answer: Hence, the solution is x = 5,-15

Conclusion

A modulus function can be used to find the magnitude of a number/variable without considering its sign. In other words, a modulus function gives the absolute value of a number. Modulus of a function f(x) is given by |x|, where x≥0. Functions can be referred to as a set of rules which produces new outputs out of given elements. Modulus of function of x, where x belongs to a real number, is given by

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

A set of all the real numbers form the domain of the modulus functions.

FAQs

1.Define the range of signum functions.

Range of the signum functions is {-1,0,1}

2.Why is modulus function positive?

The modulus of a number greater than zero is positive, and the modulus of a number less than zero is also positive irrespective of its sign. Threfore, the modulus function gives a positive value.

3.What is the vertex of the modulus functions?

The vertex of the modulus functions is (0,0) for y=|x|.

4.What is the range of the modulus functions?

A set of all numbers greater than or equal to zero is the range of modulus functions.

5.What is the derivative of modulus functions?

The Modulus function is not differentiable on the real line but on some parts of it, and the derivative of modulus function is

$$\mathrm{\frac{d\{f(x)\}}{dx}=1,if\: x>0}$$

$$\mathrm{\frac{d\{f(x)\}}{dx}=-1,if\: x<0}$$