Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Big Omega (Ω) and Big Thera (θ) Notation
Asymptotic Notations
Asymptotic notations are used to represent the complexities of algorithms for asymptotic analysis. These notations are mathematical tools to represent the complexities. There are three notations that are commonly used.
Big Omega Notation
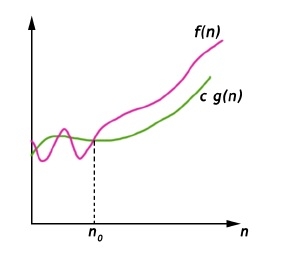
Big-Omega (Ω) notation gives a lower bound for a function f(n) to within a constant factor.
We write f(n) = Ω(g(n)), If there are positive constants n0 and c such that, to the right of n0 the f(n) always lies on or above c*g(n).
Ω(g(n)) = { f(n) : There exist positive constant c and n0 such that 0 ≤ c g(n) ≤ f(n), for all n ≤ n0}
Big Theta Notation
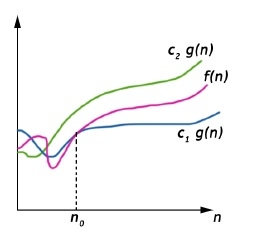
Big-Theta(Θ) notation gives bound for a function f(n) to within a constant factor.
We write f(n) = Θ(g(n)), If there are positive constants n0 and c1 and c2 such that, to the right of n0 the f(n) always lies between c1*g(n) and c2*g(n) inclusive.
Θ(g(n)) = {f(n) : There exist positive constant c1, c2 and n0 such that 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n), for all n ≥ n0}
8K+ Views
