
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Check if a graph is strongly connected - Set 1 (Kosaraju using DFS) in C++
To check a strongly connected graph using Kosaraju's algorithm, we need to understand the strongly connected graph and Kosaraju's algorithm. For a graph to be strongly connected, it should be a directed graph, and for any pair of vertices u and v in the directed graph, there exists a directed path from u to v and a directed path from v to u.
In this article, we have a directed graph with five vertices. Our task is to use Kosaraju's algorithm to check if the given graph is strongly connected or not.
Example of Strongly Connected Graph
The graph displayed in the figure below is an example of a strongly connected graph.
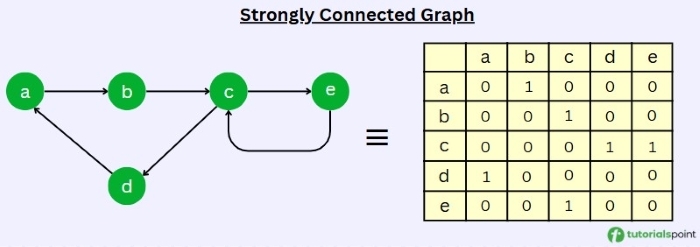
In the above graph, we can visit each node from any chosen node and traverse back. If we start from node 'a' then, a -> b -> c -> e -> c -> d -> a. Similarly, we can choose any random node to traverse the graph and also traverse back to starting node.
What is Kosaraju's Algorithm?
Kosaraju's Algorithm finds the strongly connected components (SCCs) in a directed graph. A SCC is a maximal subset of vertices such that every vertex is reachable from every other vertex within the subset. In this algorithm, we use depth-first search (DFS) twice. The first time, we traverse the original graph and once on the transposed/reversed graph.
Steps to Implement Kosaraju's Algorithm
You can use the following steps to check if the given graph is a strongly connected graph or not using Kosaraju's algorithm:
- Mark all nodes as not visited.
- Start DFS traversal from any arbitrary vertex u. If the DFS fails to visit all nodes, then return false.
- Reverse all edges of the graph and set all vertices as not visited nodes again.
- Start DFS traversal from that vertex u. If the DFS fails to visit all nodes, then return false, otherwise return true.
- If you can traverse the original graph and the reversed graph using DFS, then the given graph is the strongly connected graph.
C++ Implementation of Kosaraju's Algorithm
Here is the code implementation of the above steps to implement Kosaraju's algorithm for checking if the given directed graph is a strongly connected graph or not.
#include <iostream>
#include <list>
using namespace std;
class Graph
{
int V;
list<int> *adj;
void dfs(int v, bool visited[]);
public:
Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
~Graph()
{
delete[] adj;
}
void addEdge(int v, int w);
bool isStronglyConnected();
Graph reverseArc();
};
void Graph::dfs(int v, bool visited[])
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
dfs(*i, visited);
}
Graph Graph::reverseArc()
{
Graph graph(V);
for (int v = 0; v < V; v++)
{
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
graph.adj[*i].push_back(v);
}
return graph;
}
void Graph::addEdge(int u, int v)
{
adj[u].push_back(v);
}
bool Graph::isStronglyConnected()
{
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
Graph graph = reverseArc();
for (int i = 0; i < V; i++)
visited[i] = false;
graph.dfs(0, visited);
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
int main()
{
Graph graph(5);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
graph.addEdge(3, 0);
graph.addEdge(2, 4);
graph.addEdge(4, 2);
graph.isStronglyConnected() ? cout << "This is strongly connected" : cout << "This is not strongly connected";
}
The output of the above code is as follows:
This is strongly connected
Complexity to Check Strongly Connected Graph
- Time Complexity: The time complexity of Kosaraju's algorithm for checking if the given directed graph is strongly connected is O(V + E).
- Space Complexity: The space complexity of Kosaraju's algorithm for checking if the given directed graph is strongly connected is O(V + E).

