Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Secant method to solve non-linear equation
Secant method is also used to solve non-linear equations. This method is similar to the Newton-Raphson method, but here we do not need to find the differentiation of the function f(x). Only using f(x), we can find f’(x) numerically by using Newton’s Divide difference formula. From the Newton-Raphson formula,
we know that,
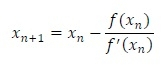
Now, using divide difference formula, we get,
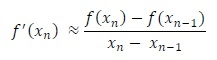
By replacing the f’(x) of Newton-Raphson formula by the new f’(x), we can find the secant formula to solve non-linear equations.
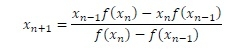
Note: For this method, we need any two initial guess to start finding the root of non-linear equations.
Input and Output
Input: The function f(x) = (x*x) - (4*x) - 10 Output: The root is: -1.74166
Algorithm
secant(x1, x2)
Input: Two initial guess for root.
Output: The approximate root of a non-linear equation f(x).
Begin f1 := f(x1) f2 := f(x2) x3 := ((f2*x1) – (f1*x2)) / (f2 – f1) while relative error of x3 and x2 are > precision, do x1 := x2 f1 := f2 x2 := x3 f2 := f(x2) x3 := ((f2*x1) – (f1*x2)) / (f2 – f1) done root := x3 return root End
Example
#include<iostream>
#include<cmath>
using namespace std;
double absolute(double value) { //to find magnitude of value
if(value < 0)
return (-value);
return value;
}
double f(double x) { //the given function x^2-4x-10
return ((x*x)-(4*x)-10);
}
double secant(double x1, double x2) {
double x3, root;
double f1, f2;
f1 = f(x1);
f2 = f(x2);
x3 = (f2*x1-f1*x2)/(f2-f1);
while(absolute((x3-x2)/x3) > 0.00001) { //test accuracy of x3
x1 = x2; //shift x values
f1 = f2;
x2 = x3;
f2 = f(x2); //find new x2
x3 = (f2*x1-f1*x2)/(f2-f1); //calculate x3
}
root = x3;
return root; //root of the equation
}
main() {
double a, b, res;
a = 0.5;
b = 0.75;
res = secant(a, b);
cout << "The root is: " << res;
}Output
The root is: -1.74166
Updated on: 17-Jun-2020
903 Views
Advertisements