Implementation of Jacobi Method to Solve a System of Linear Equations in Python

It is the most straightforward iterative strategy for tackling systems of linear equations shown below.

$$\mathrm{a_{1,1}\: x_{1} \: + \: a_{1,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{1,n} \: x_{n} \: = \: b_{1}}$$

$$\mathrm{a_{2,1} \: x_{1} \: + \: a_{2,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{2,n} \: x_{n} \: = \: b_{2}}$$

$$\mathrm{\vdots}$$

$$\mathrm{a_{n,1} \: x_{1} \: + \: a_{n,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{n,n} \: x_{n} \: = \: b_{n}}$$

The fundamental concept is: each linear equation is reorganised by shifting a new variable to the left side. The new values are then determined starting with an initial guess for each variable. During the following iteration, the new values will be used as an educated guess. Up until each variable's convergence condition is satisfied, this iteration process is repeated till a final converged answer is obtained.

The Jacobi's Algorithm

The Jacobi's algorithm is as follows −

• Start with some initial array of guesses for the unknowns (x).

• Evaluate new x’s by substituting guess values for x’s in the rearranged form of equations as shown below −

$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{guess}} \: − \: b_{i})}$$

Now the $\mathrm{x_{i_{new}}}$ will be the new x value obtained from the current iteration.

• The next step is to evaluate the error between the new and guess values, i.e., $\mathrm{\lvert x_{new} \: − \: x_{guess} \rvert}$. If the error is more than some convergence criterion (we have taken it as $\mathrm{10^{−5}}$), then assign new values to the old guess i.e. $\mathrm{x_{guess} \: = \: x_{new}}$ and then start the next iteration.

• Else, $\mathrm{x_{new}}$ is the final answer.

Jacobi's Algorithm – An Example

Let us demonstrate the algorithm with the help of the following example −

$$\mathrm{20x \: + \: y \: − \: 2z \: = \: 17}$$

$$\mathrm{3x \: + \: 20y \: − \: z \: = \: −18}$$

$$\mathrm{2x \: − \: 3y \: + \: 20z \: = \: 25}$$

Rearranging the above equations as follows −

$$\mathrm{x_{new} \: = \: (−y_{guess} \: + \: 2z_{guess} \: + \: 17)/20}$$

$$\mathrm{y_{new} \: = \: (−3x_{guess} \: + \: z_{guess} \: − \: 18)/20}$$

$$\mathrm{z_{new} \: = \: (−2x_{guess} \: + \: 3y_{guess} \: + \: 25)/20}$$

Now these equations will be solved in the while loop to obtain new value of unknowns based on the guess value.

Python Program to Implement Jacobi's Method

The program to implement the Jacobi's method (equation wise implementation) is shown below −

Example

# Importing module for plotting and array
from pylab import *
from numpy import *

# Initial guess to start with
xg=0
yg=0
zg=0

# Setting error to move into the while loop
error=1

# Setting up iteration counter
count=0

while error>1.E-5:
   count+=1
    
   #Evaluating new values based on old guess
   x=(17-yg+2*zg)/20
   y=(zg-18-3*xg)/20
   z=(25-2*xg+3*yg)/20

   # Error evaluation and plotting
   error = abs(x-xg)+abs(y-yg)+abs(z-zg)
   figure(1,dpi=300)
   semilogy(count,error,'ko')
   xlabel('iterations')
   ylabel('error')

   # Updating the Guess for next iteration.
   xg=x
   yg=y
   zg=z

savefig('error_jacobi.jpg')
print(f'x={round(x,5)}, y={round(y,5)}, z={round(z,5)}')

Output

The program output will be

$$\mathrm{x \: = \: 1.0 \: , \: y \: = \: −1.0 \: , \: z \: = \: 1.0}$$

The variation of error with every iteration count is shown in the figure given below −

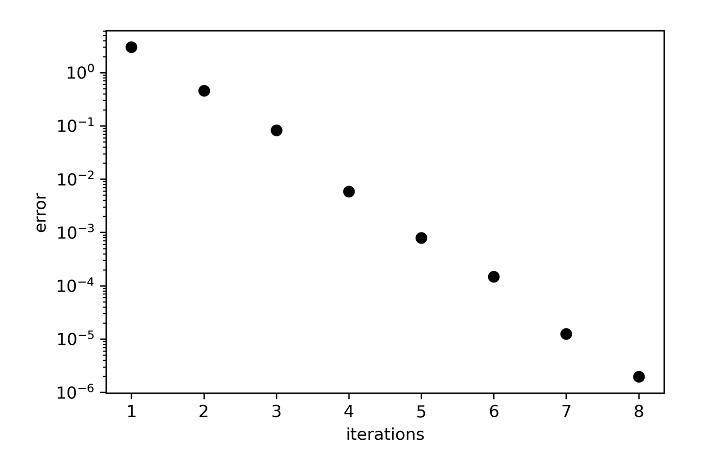
One can observe that the converged solution is arrived at 8th iteration.

But, I think it will be better that if we can enter the elements of the system of linear equation in a matrix and solve them in a matrix fashion rather than in equation form. So, the procedural code to perform this task is as follows −

Example

# Importing module
from pylab import *
from numpy import *

#-----------------------------------------#
# Array of coefficients of x
a=array([[20,1,-2],[3,20,-1],[2,-3,20]])

# Array of RHS vector
b=array([17,-18,25])

# Number of rows and columns
n=len(b)
#-----------------------------------------#


# Setting up the initial guess array
xg=zeros(len(b))

# Starting error to enter in loop
error=1

# Setting iteration counter
count=0

# Generating array for new x
xn=empty(len(b)) 
#-----------------------------------------#


while error>1.E-5:
   count+=1
   for i in range(n):
      sum1=0
      for j in range(n):
         if i!=j:
            sum1=sum1+a[i,j]*xg[j]
      xn[i]=(-1/a[i,i])*(sum1-b[i])


   # Error evaluation and plotting
   error = sum(abs(xn-xg))
    
   figure(1,dpi=300)
   semilogy(count,error,'ko')
   xlabel('iterations')
   ylabel('error')

   # Substituting new value as the Guess for next iteration
   xg=xn.copy()
#-----------------------------------------#

savefig('error_jacobi.jpg')
print('x: ',xn)

Output

x: [ 1.00000007 -0.99999983 1.00000005]

Conclusion

In this tutorial, we explained how you can use Python to model Jacobi's iteration method to solve simultaneous linear equations. Two approaches were discussed namely; equation approach and matrix approach.