Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum edges required to add to make Euler Circuit in C++
Concept
With respect of a given undirected graph of b nodes and a edges, the job is to determine minimum edges needed to build Euler Circuit in the given graph.
Input
b = 3,
a = 2
Edges[] = {{1, 2}, {2, 3}}Output
1
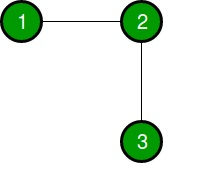
By connecting 1 to 3, we can build a Euler Circuit.
Method
With respect of a Euler Circuit to exist in the graph we need that every node should haveeven degree because then there exists an edge that can be applied to exit the node after entering it.
Now, there can be two cases −
Existence of one connected component in the graph
With respect of this case, if all the nodes in the graph is equipped with even degree then we say that the graph already have a Euler Circuit and we don’t require to add any edge in it. But if there is any node equipped with odd degree we require adding edges.Even number of odd degree vertices can be exist in the graph. This incident can be easilyverified by the fact that the sum of degrees from the even degrees node and degrees fromodd degrees node should match the total degrees that is always even as every edge contributes two to this sum. As a result of this, if we pair up random odd degree nodes in the graph and add an edge between them we can build all nodes to have even degree and thus build an Euler Circuit exist.
Existence of disconnected components in the graph
At first we mark component as odd and even. Odd components are those which have minimumone odd degree node in them. Now we take all the even components and choose a random vertex from every component and arrange them up linearly. So adding an edge between adjacent vertices,we have connected the even components and built an equivalent odd component that has two nodes with odd degree.
As a result of this,to deal with odd components i.e components with minimum one odd degree node, we can connect all these odd components applying edges whose number is equalto the number of disconnected components. This can be accomplished by placing the components in the cyclic order and selecting two odd degree nodes from every component and applying these to connect to the components on either side. Now we have a single connected component for which we have explained.
Example
//This C++ program finds minimum edge required
// to make Euler Circuit
#include <bits/stdc++.h>
using namespace std;
// This Depth-First Search finds a connected
// component
void dfs1(vector<int> g1[], int vis1[], int odd1[],
int deg1[], int comp, int v){
vis1[v] = 1;
if (deg1[v]%2 == 1)
odd1[comp]++;
for (int u : g1[v])
if (vis1[u] == 0)
dfs1(g1, vis1, odd1, deg1, comp, u);
}
// We return minimum edge required to build Euler
// Circuit
int minEdge1(int n, int m, int s1[], int d1[]){
// g1 : to store adjacency list
// representation of graph.
// e1 : to store list of even degree vertices
// o1 : to store list of odd degree vertices
vector<int> g1[n+1], e1, o1;
int deg1[n+1]; // Degrees of vertices used
int vis1[n+1]; // To store visited in DFS
int odd1[n+1]; // Number of odd nodes in components
memset(deg1, 0, sizeof(deg1));
memset(vis1, 0, sizeof(vis1));
memset(odd1, 0, sizeof(odd1));
for (int i = 0; i < m; i++){
g1[s1[i]].push_back(d1[i]);
g1[d1[i]].push_back(s1[i]);
deg1[s1[i]]++;
deg1[d1[i]]++;
}
// This 'ans' is result and 'comp' is component id
int ans = 0, comp = 0;
for (int i = 1; i <= n; i++){
if (vis1[i]==0){
comp++;
dfs1(g1, vis1, odd1, deg1, comp, i);
// We check that if connected component
// is odd.
if (odd1[comp] == 0)
e1.push_back(comp);
// We check that if connected component
// is even.
else
o1.push_back(comp);
}
}
// It has been seen that if whole graph is a single connected
// component with even degree.
if (o1.size() == 0 && e1.size() == 1)
return 0;
// It has been seen that if all connected component is even
if (o1.size() == 0)
return e1.size();
//It has been seen that if graph have atleast one even connected
// component
if (e1.size() != 0)
ans += e1.size();
// For all the odd connected component.
for (int i : o1)
ans += odd1[i]/2;
return ans;
}
// Driven Program
int main(){
int b = 3, a = 2;
int source1[] = { 1, 2 };
int destination1[] = { 2, 3 };
cout << minEdge1(b, a, source1, destination1) << endl;
return 0;
}Output
1
161 Views
