What is the full form of BCD ?

Definition and Explanation of (BCD)

A technique for converting decimal integers into their binary equivalents is called Binary Coded Decimals (BCD).

• A collection of bits is used to represent each decimal digit

• You can use either 4-bits or 8-bit for this encoding.

• It is a rapid and efficient way to transform input values into binary digits when contrasted with the existing binary system.

• In digital displays where changing data may be difficult, they are frequently used.

• Since each digit is controlled as a separate single sub-circuit in this scenario, BCD is absolutely essential.

The BCD equivalent of each decimal digit in the integer and fractional parts of the number is its four-bit binary value. The 8421 BCD code is another name for the BCD code. The weights of the different bits in the four-bit groups, from the MSB to the LSB, are represented by the numbers 8, 4, 2, and 1.

When encoded in binary, some decimal numbers have infinite place values, while they only have limited place values in decimal. The binary representation of the number 0.2 is .001100, and the BCD representation is 0.0010.

Look closely at how the truth table below depicts this −

Example: BCD conversion for (321)10

According to the truth table above,

3 = 0011

2 = 0010

1 = 0001

As a result, BCD = 0011 0010 0001

BCD and Digital Systems: Purpose and Usage

A 4-bit binary integer called the "binary coded decimal" is specifically designed to represent a decimal number.

Usage

The fundamental benefit of using binary-coded decimals to represent decimal values in digital systems is its simplicity in converting between decimal and binary representations. A four-bit number represents each decimal digit in binary coded decimal (BCD), and a weighted sum of binary values can also represent each digit.

BCD and Computer Science: Applications and Examples

BCD, or binary-coded decimal, is the four-digit binary representation of the numbers 0 through 9, commonly referred to as "packet decimal." BCD was used by several early decimal computers, such as the IBM System/360 series. It is used to add BCD numbers. For a BCD digit, there are 10 alternative four-bit representations.

BCD Adder in Digital Logic

Consider that A and B are four-bit numbers. The values of A and B for decimal integers can range from 0 (0000 in binary) through 9 (1001 in binary). If the carry from the previous total is disregarded, the output will range from 0 to 18. Therefore, if the carry is taken into account, the output will have a maximum value of 19 (9 + 9 + 1 = 19). When we just add A and B, we get the binary sum. In this case, we'll use the BCD adder to get the result in BCD format.

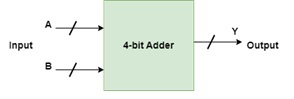
Representation of BCD adder in Digital Logic

Description: Illustration depicts the use of BCD in Computer Science

Example -

Input : A = 0101 B = 1001

Output : Y = 1 0100

Explanation: The two numbers A (= 5) and B (= 9) are being added.

1110 (= 14) will be the binary sum's value.

Yet since the binary value of 1 is 0001 and the binary value of 4 is 0100, the BCD sum will be 1 0100.

BCD and Data Storage: Advantages and Disadvantages

Advantages

Binary-coded decimals are useful for digital displays, where it may be difficult to handle or display large numbers. The fact that a binary-coded decimal sees each digit as a separate subcircuit makes it easier to manage data in such devices. On such panels, integrated circuits can be configured to produce binary-coded decimal numerals.

Disadvantages

Binary-coded decimal has certain disadvantages in addition to their advantages. Encoding a decimal number as a binary-coded decimal wastes space in a computer's memory and is an inefficient way to store numbers. Also, compared to the traditional binary system, it necessitates more complex circuitry. Binary-coded decimal coding can also be wasteful since a number of 4-bit states (10 to 16) are inefficient.

Conclusion

In binary-coded decimal, each digit of a base-10 integer is represented by a group of four binary digits or bits. Each base-10 number or digit can be shown in binary format when using binary-coded decimals. It is clear that all the BCD does is give each decimal digit a binary representation. The specified decimal value is heavier and requires more bits in its BCD representation.

FAQs

Q1. What are the types of BCD?

Ans. There are two varieties of the binary-coded decimal.

Unpacked BCD

On a computer, each 4-bit group of an unpacked binary-coded decimal number is stored in its own register. This has the drawback of using up less storage space for the binary-coded decimal integers if the registers are 8 bits wide or wider.

Packed BCD

Two binary-coded decimal digits are packed into an 8-bit register as values. It is possible to store two binary-coded decimal numbers in a single register by relocating the number in the higher register four times to the left and then combining the numbers in the upper and lower registers.

Q2. What is the difference between BCD and simple binary representation?

Ans. In a straightforward binary representation, the entire number is divided repeatedly by 2 to create its binary form. Each individual digit is converted to binary in binary-coded decimal. Each digit is then converted to its 4-bit binary counterpart before being combined.

Here's an illustration:

234, in decimal form.

The binary representation is 234: 11101010

234 is represented in binary-coded decimal as follows:

2 = 0010, 3 = 0011, 4 = 0100

Therefore, 234 = 001000110100

Q3. What is the BCD representation of (4589)10?

Ans. BCD conversion for (4589)10

According to the truth table above,

4 = 0100

5 = 0101

8 = 1000

9 = 1001

As a result, BCD = 0100010110001001