Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Blocking Networks and Non-Blocking Networks in Computer Architecture?
Blocking Networks
Blocking networks possess the property that in the presence of a currently established interconnection between a pair of input/output, the arrival of a request for a new interconnection between two arbitrary unused input and output may or may not be possible. Examples of blocking networks include Omega, Banyan, Shuffle–Exchange, and Baseline. Consider, for example SEN, as shown in the figure.
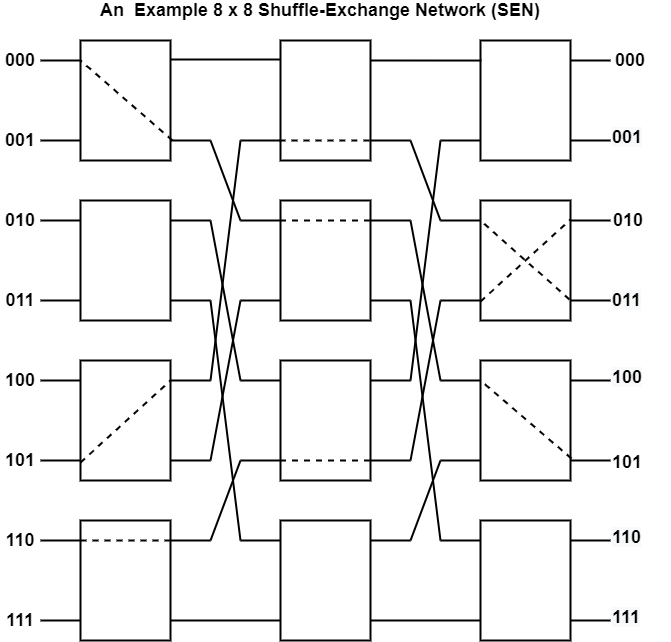
In the presence of a connection between input 101 and output 011, a connection between input 100 and output 001 is not possible. This is because the connection 101 to 011 uses the upper output of the third switch from the top in the first stage. This same output will be needed by the requested connection 100 to 001. This contention will lead to the inability to satisfy the connection 100 to 001 that is, blocking. While connection 101 to 011 is established, the arrival of a request for a connection such as 100 to 110 can be satisfied.
Rearrangeable Networks
Rearrangeable networks are characterized by the property that it is always possible to rearrange already established connections to make allowance for other connections to be established simultaneously. The Benes is a well-known example of rearrangeable networks.
Nonblocking Networks
Nonblocking networks are characterized by the property that in the presence of a currently established connection between any pair of input/output, it will always be possible to establish a connection between any arbitrary unused pair of input/output. The Clos is a well-known example of nonblocking networks.
It consists of r1n1 x m input crossbar switches (r1 is the number of input crossbars, and n1 x m is the size of each input crossbar), mr1x r2 middle crossbar switches (m is the number of middle crossbars, and r1 x r2 is the size of each middle crossbar), and r2m x n2 output crossbar switches (r2 is the number of output crossbars and m x n2 is the size of each output crossbar). The Clos network is not blocking if the following inequality is satisfied m ≥ n1 + n2 − 1.
3K+ Views
