Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Bipolar Encoding?
The bipolar encoding scheme defines three voltage methods: positive, negative, and zero. In the Bipolar encoding scheme, zero levels define binary 0, and binary 1 is described by rotating positive and negative voltages.
Assume the first 1 bit is described by positive amplitude. A negative voltage means the second 1 bit; the positive amplitude explains the third 1 bit. This rotation can also appear even when the 1 bits are not successive.
There are three types of Bipolar which are as follows −
AMI
AMI means Bipolar Alternate Mark Inversion. It is the elementary method of bipolar encoding. Here the word 'mark' comes from telegraphy defines 1. AMI defines alternate 1 inversion.
In the Bipolar AMI encoding scheme, 0 bit is defined by zero levels and 1 bit is described by rotating positive and negative voltages.
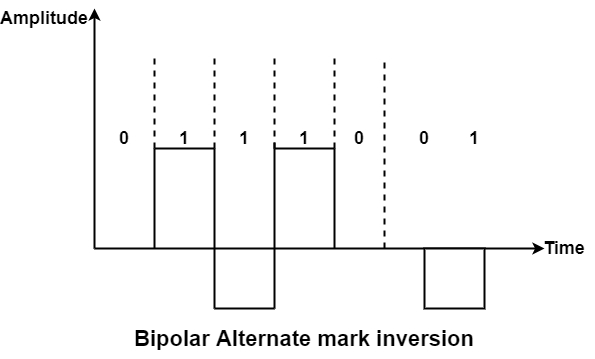
A variation of bipolar AMI is also known as pseudo ternary because binary 0 alternates between +ve and –ve voltages. By reversing each appearance of a 1, bipolar AMI achieves two things, the DC component is zero, and the second stay synchronized. Still, long strings of the synchronization method are not ensured.
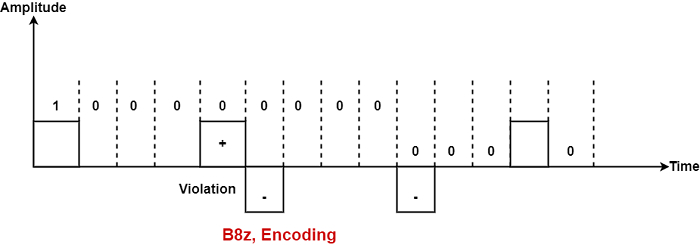
B8ZS
B8ZS stands for Bipolar 8-Zero Substitution. This is identical to bipolar AMI. Bipolar AMI changes poles with each '1' it encounters. But the signal does not modify during a string of 0’s. So, where synchronization is minimum in AMI.
But in B8ZS, wherever eight or more consecutive 0’s are encountered in the DataStream, the design depends on the polarity of the previous 1 is the same (that is occurring just before 8 0’s) as shown in the figure −
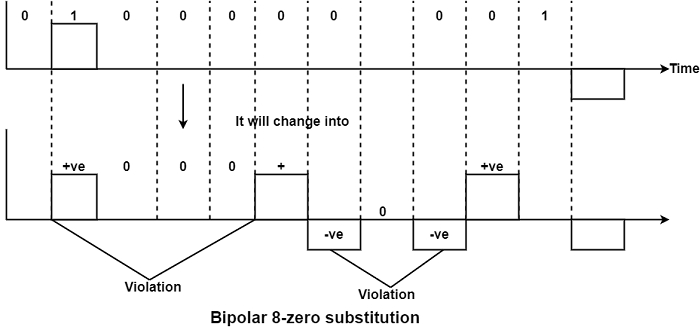
So in blank of (8) zero’s, there are two cases either the polarity of 1 before zero is +ve or –ve then the solution of both cases will be as follows −
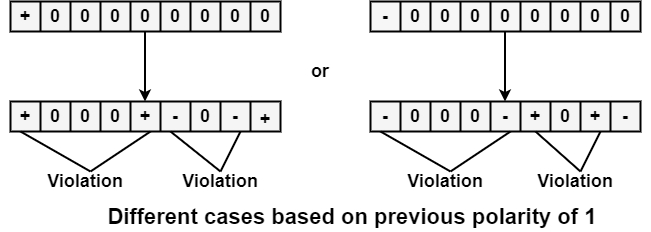
So in both cases, we have violated two times consecutively two +ve and consecutively two –ve appears when fourth, fifth, seven and eight zeros are polarity changes.
HDB3
HDB3 represents High-Density Bipolar 3. The issue of synchronizing strings of successive 0’s is HDB3. It changes forever four consecutive zeros encountered into the bipolar AMI pattern.
An example is shown for every four consecutive zero’s pattern with two cases.
Case 1 − If the number of 1’s since the final substitution is odd.
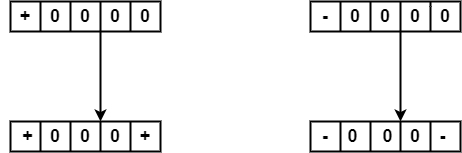
Case 2: If the number of 1’s since the final substitution is even.
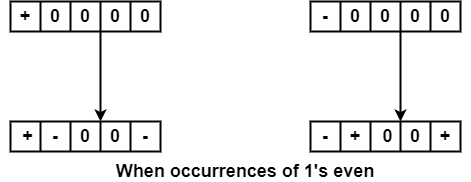
As in B8ZS, the violation pattern in HDB3 depends on the last bit '1' polarity. But in HDB3, it also looks the number of 1’s have occurred in the bitstream since the previous substitution. If the number of 1’s from the last substitution is odd, HDB3 inserts a violation in the fourth successive zero places. But if the previous substitution is even, HDB3 put violation in the first and fourth consecutive zero positions.
Example − Using B8ZS, encode the Bitstream 10000000000010
5K+ Views
