Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
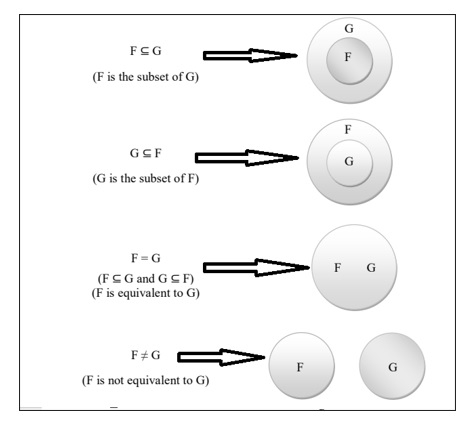
What is an equivalence of sets of functional dependencies?
A set of functional dependencies (FD) F is said to cover another set of functional dependencies E if every FD in E is also in F closure; that is, if every dependency in E can be inferred from F.
Alternatively, we can say E is covered by F. Two sets of functional dependencies E and F are equivalent if E+= F+. That is E is equivalent to F if E covers F and F covers E.
To determine whether F covers E we calculate X+ with respect to F for each FD X->y in E and then check whether X+ includes the attributes Y.
Example
R=(A,B,C,D,E,F)
F1={A->BC, B->CDE, AE->F}
F2={A->BCF, B->DE, E->AB}
Check whether F1 and F2 are equivalent or not.
Solution
To check F1 covers F2 −
A+={A,B,C,D,E,F} contains B,C,F
B+={B,C,D,E} contains D,E
E+={E} contains A,B
So F1 does not cover F2.
Hence F1 and F2 are not equivalent.
Example
Consider another example where two functional dependencies are equivalent.
R=(A,C,D,E,H)
F1={A->C, AC->D, E->AD, E->H},
F2={A->CD, E->AH}
Check whether F1 and F2 are equivalent or not?
Solution
To check F1 covers F2 −
A+={A,C,D} contains C,D
E+={A,D,E,H} contains A,H
So F1 covers F2
To check F2 covers F1:
A+={A,C,D} contains C
{ A,C}+={A,C,D} contains D
E+={A,C,D,E,H} contains A,D,H
So F2 covers F1.
Hence F1 and F2 are equivalent.
This is represented diagrammatically as follows −
5K+ Views
