Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Tree or Connected acyclic graph
Trees are graphs that do not contain even a single cycle. They represent hierarchical structure in a graphical form. Trees belong to the simplest class of graphs. Despite their simplicity, they have a rich structure.
Trees provide a range of useful applications as simple as a family tree to as complex as trees in data structures of computer science.
Tree
A connected acyclic graph is called a tree. In other words, a connected graph with no cycles is called a tree.
The edges of a tree are known as branches. Elements of trees are called their nodes. The nodes without child nodes are called leaf nodes.
A tree with 'n' vertices has 'n-1' edges. If it has one more edge extra than 'n-1', then the extra edge should obviously has to pair up with two vertices which leads to form a cycle. Then, it becomes a cyclic graph which is a violation for the tree graph.
Example 1
The graph shown here is a tree because it has no cycles and it is connected. It has four vertices and three edges, i.e., for 'n' vertices 'n-1' edges as mentioned in the definition.
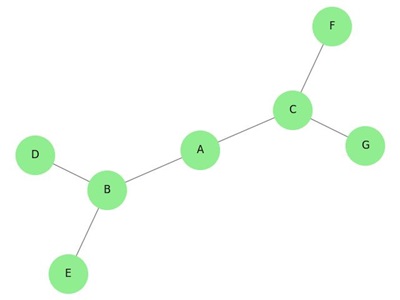
Note − Every tree has at least two vertices of degree one.
Example 2
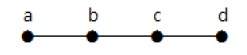
In the above example, the vertices 'a' and 'd' has degree one. And the other two vertices 'b' and 'c' has degree two. This is possible because for not forming a cycle, there should be at least two single edges anywhere in the graph. It is nothing but two edges with a degree of one.
Forest
A disconnected acyclic graph is called a forest. In other words, a disjoint collection of trees is called a forest.
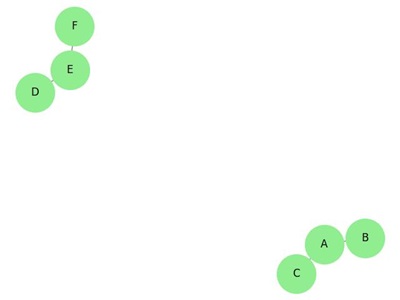
Example
The following graph looks like two sub-graphs; but it is a single disconnected graph. There are no cycles in this graph. Hence, clearly it is a forest.
Spanning Trees
Let G be a connected graph, then the sub-graph H of G is called a spanning tree of G if −
- H is a tree
- H contains all vertices of G.
A spanning tree T of an undirected graph G is a subgraph that includes all of the vertices of G.
Example
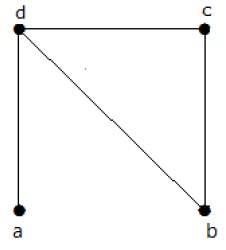
In the above example, G is a connected graph and H is a sub-graph of G.
Clearly, the graph H has no cycles, it is a tree with six edges which is one less than the total number of vertices. Hence H is the Spanning tree of G.
1K+ Views
