
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Generate a Random Directed Acyclic Graph (DAG) for a Given Number of Edges
A Directed Acyclic Graph or DAG is a directed graph (a graph where each edge has a direction) that has no cycles present i.e. if we traverse along the direction of the edges then no closed loops are formed along any path. A DAG is always topologically ordered, i.e. for each edge in the graph, the start vertex of the edge(u) occurs earlier in the sequence than the ending vertex(v) of the edge i.e.(u<v).
In this article, our task is to generate a random Directed Acyclic Graph having 'N' node and 'E' edges in C++. The figure given below demonstrates an example of DAG:
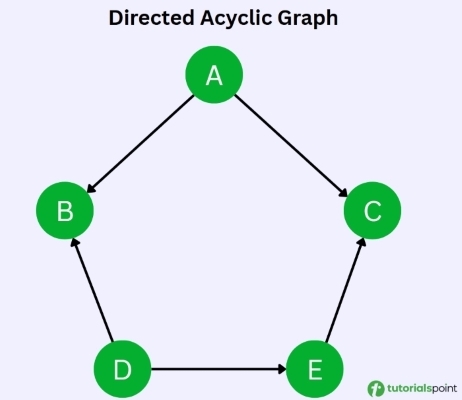
The above Directed Acyclic graph can be represented as:
A -> {B C}
B -> {Isolated Vertex}
C -> {Isolated Vertex}
D -> {B E}
E -> {C}
Steps to Generate Random Directed Acyclic Graph
The steps to generate the random directed acyclic graph are as follows:
- First, we specify the number of nodes and edges that we want in our graph.
- Then we check the conditions for Directed Acyclic Graph, i.e., the graph should have direction and it should not contain any cycles.
- To check if the graph is directed and acyclic, we make sure that the source node(u) is less than the destination node(v). This prevents the cycle in the graph.
- Then, for random edge generation, we have used the rand() function. The while loop keeps generating the edges until all the edges are generated (edges.size() < E).
- Then, we check that no duplicate edge is formed. We have used a for loop to check if the source node and destination node are the same. If the source and destination node are the same, then we break the loop and mark it as true, meaning the edge already exists in the graph.
- Then we have printed the randomly generated DAG. The found variable checks if the source node (u) exist in the edges.
- If the source node exist then print the edge of source node and its respective destination node and mark it as true. If the source node (u) is marked as false, then print a message "Isolated vertex".
C++ Implementation of Random DAG
The following example generates a random directed acyclic graph using the above steps:
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
#define N 5 // Number of vertices
#define E 5 // Number of edges to generate
void GenerateRandomDAG()
{
srand(time(0));
vector<pair<int, int>> edges;
int attempts = 0;
while (edges.size() < E && attempts < E * 5)
{
int u = rand() % N;
int v = rand() % N;
// Ensure direction u ? v is acyclic (u < v)
if (u >= v)
continue;
// Avoid duplicate edges
bool exists = false;
for (auto edge : edges)
{
if (edge.first == u && edge.second == v)
{
exists = true;
break;
}
}
if (!exists)
{
edges.emplace_back(u, v);
}
attempts++;
}
// Print the DAG
cout << "Generated Random Directed Acyclic Graph:\n";
for (int i = 0; i < N; ++i)
{
cout << "\t" << i << " -> { ";
bool found = false;
for (auto edge : edges)
{
if (edge.first == i)
{
cout << edge.second << " ";
found = true;
}
}
if (!found)
cout << "Isolated Vertex!";
cout << " }\n";
}
}
int main()
{
GenerateRandomDAG();
return 0;
}
The output of the above code is as follows:
Generated Random Directed Acyclic Graph:
0 -> { 2 }
1 -> { 4 2 }
2 -> { 3 }
3 -> { 4 }
4 -> { Isolated Vertex! }
Complexity of Directed Acyclic Graph
- Time Complexity: The time complexity of the Directed Acyclic Graph is O(E*E+N*E) or O(E^2).
- Space Complexity: The space complexity of the Directed Acyclic Graph is O(E).

