The time when the minute hand and the hour hand coincide after a given hour

When the minute hand moves from 12 to 12 in one hour, the hour hand also moves from the previous hour to the next.

Hence, every hour, the minute hand and the hour hand coincide once.

Problem Statement

Given an input hour, find the time in minutes when the hour hand and the minute hand coincide within the next hour.

Examples

Input − Hour = 4

Output − Coinciding time: 240/11 minutes.

We will discuss the explanation further with the approach.

Input − Hour = 5

Output − Coinciding time: 300/11 minutes.

Explanation and the Approach

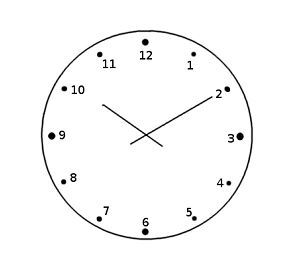
When the minute hand moves a complete circle in an hour, the hour hand also moves from one hour to another hour. Thus, mathematically speaking −;

When the minute hand moves 60 minutes, the hour hand moves 5 minutes.

OR −

When the minute hand takes 60 steps, the hour hand takes 5 steps.

Hence −

60 steps of minute hand == 5 steps of hour hand

Thus −

1 step of minute hand = 1/12 steps of hour hand

Now, let’s say that it takes m minutes for the hour and the minute hand to coincide.

If the input hour is h −

Then the minute hand has to move h*5 minutes plus the minutes the hour hand has covered starting from that hour.

Hence, m = h*5 + m/12. (m/12 = minutes the hour hand has covered from the starting input hour).

Taking LCM −

m = (h*5*12 + m)/12

12m = 60*h + m

12m-m = 60*h

11m = 60*h

Hence, m = 60*h/11

Now, let’s consider the above examples and verify the formula.

• Input Hour = 4

The time (in minutes) when the hour hand and the minute hand will coincide will be:

m = 60*hour/11

Hence, m = 60*4/11

m = 240/11 minutes.

• Similarly, for input hour = 5,

m = 60*5/11

I.e. 300/11 minutes.

We can use the above formula and code our solution.

Pseudo Code

main():

• Initialize the input hour.

• Call the function coinciding_time(hour).

coinciding_time(int hour):

• time -> 60*hour/11

• Print time.

Example

Below is a C++ Program to find the time when the minute hand and the hour hand coincide after a given hour.

#include<bits/stdc++.h>
using namespace std;
//Function to find the time in minutes.
void coincide_time(int hour){
   //Temporary variable
   int temp = 60*hour;
   cout<<"Coinciding time: ";
   cout<< temp<<"/"<<11<<" minutes"<<endl;
}
int main(){
   //Initialize the input hour
   int hour = 8;
   //Function call
   coincide_time(hour);
   return 0;
}

Output

Coinciding time: 480/11 minutes

Analysis

Time Complexity − O(1) [Constant]

Space Complexity − O(1) [Constant]

Conclusion

In this article, we found out the time when the hour hand and the minute hand coincide. We derived the formula using the unitary method and understood it using a few examples. Then, we used the formula to write a pseudocode and program the solution in C++.