
- Digital Electronics - Home
- Digital Electronics Basics
- Types of Digital Systems
- Types of Signals
- Logic Levels And Pulse Waveforms
- Digital System Components
- Digital Logic Operations
- Digital Systems Advantages
- Number Systems
- Number Systems
- Binary Numbers Representation
- Binary Arithmetic
- Signed Binary Arithmetic
- Octal Arithmetic
- Hexadecimal Arithmetic
- Complement Arithmetic
- Base Conversions
- Base Conversions
- Binary to Decimal Conversion
- Decimal to Binary Conversion
- Binary to Octal Conversion
- Octal to Binary Conversion
- Octal to Decimal Conversion
- Decimal to Octal Conversion
- Hexadecimal to Binary Conversion
- Binary to Hexadecimal Conversion
- Hexadecimal to Decimal Conversion
- Decimal to Hexadecimal Conversion
- Octal to Hexadecimal Conversion
- Hexadecimal to Octal Conversion
- Binary Codes
- Binary Codes
- 8421 BCD Code
- Excess-3 Code
- Gray Code
- ASCII Codes
- EBCDIC Code
- Code Conversion
- Error Detection & Correction Codes
- Logic Gates
- Logic Gates
- AND Gate
- OR Gate
- NOT Gate
- Universal Gates
- XOR Gate
- XNOR Gate
- CMOS Logic Gate
- OR Gate Using Diode Resistor Logic
- AND Gate vs OR Gate
- Two Level Logic Realization
- Threshold Logic
- Boolean Algebra
- Boolean Algebra
- Laws of Boolean Algebra
- Boolean Functions
- DeMorgan's Theorem
- SOP and POS Form
- POS to Standard POS Form
- Minimization Techniques
- K-Map Minimization
- Three Variable K-Map
- Four Variable K-Map
- Five Variable K-Map
- Six Variable K-Map
- Don't Care Condition
- Quine-McCluskey Method
- Min Terms and Max Terms
- Canonical and Standard Form
- Max Term Representation
- Simplification using Boolean Algebra
- Combinational Logic Circuits
- Digital Combinational Circuits
- Digital Arithmetic Circuits
- Multiplexers
- Multiplexer Design Procedure
- Mux Universal Gate
- 2-Variable Function Using 4:1 Mux
- 3-Variable Function Using 8:1 Mux
- Demultiplexers
- Mux vs Demux
- Parity Bit Generator and Checker
- Comparators
- Encoders
- Keyboard Encoders
- Priority Encoders
- Decoders
- Arithmetic Logic Unit
- 7-Segment LED Display
- Code Converters
- Code Converters
- Binary to Decimal Converter
- Decimal to BCD Converter
- BCD to Decimal Converter
- Binary to Gray Code Converter
- Gray Code to Binary Converter
- BCD to Excess-3 Converter
- Excess-3 to BCD Converter
- Adders
- Half Adders
- Full Adders
- Serial Adders
- Parallel Adders
- Full Adder using Half Adder
- Half Adder vs Full Adder
- Full Adder with NAND Gates
- Half Adder with NAND Gates
- Binary Adder-Subtractor
- Subtractors
- Half Subtractors
- Full Subtractors
- Parallel Subtractors
- Full Subtractor using 2 Half Subtractors
- Half Subtractor using NAND Gates
- Sequential Logic Circuits
- Digital Sequential Circuits
- Clock Signal and Triggering
- Latches
- Shift Registers
- Shift Register Applications
- Binary Registers
- Bidirectional Shift Register
- Counters
- Binary Counters
- Non-binary Counter
- Design of Synchronous Counter
- Synchronous vs Asynchronous Counter
- Finite State Machines
- Algorithmic State Machines
- Flip Flops
- Flip-Flops
- Conversion of Flip-Flops
- D Flip-Flops
- JK Flip-Flops
- T Flip-Flops
- SR Flip-Flops
- Clocked SR Flip-Flop
- Unclocked SR Flip-Flop
- Clocked JK Flip-Flop
- JK to T Flip-Flop
- SR to JK Flip-Flop
- Triggering Methods:Flip-Flop
- Edge-Triggered Flip-Flop
- Master-Slave JK Flip-Flop
- Race-around Condition
- A/D and D/A Converters
- Analog-to-Digital Converter
- Digital-to-Analog Converter
- DAC and ADC ICs
- Realization of Logic Gates
- NOT Gate from NAND Gate
- OR Gate from NAND Gate
- AND Gate from NAND Gate
- NOR Gate from NAND Gate
- XOR Gate from NAND Gate
- XNOR Gate from NAND Gate
- NOT Gate from NOR Gate
- OR Gate from NOR Gate
- AND Gate from NOR Gate
- NAND Gate from NOR Gate
- XOR Gate from NOR Gate
- XNOR Gate from NOR Gate
- NAND/NOR Gate using CMOS
- Full Subtractor using NAND Gate
- AND Gate Using 2:1 MUX
- OR Gate Using 2:1 MUX
- NOT Gate Using 2:1 MUX
- Memory Devices
- Memory Devices
- RAM and ROM
- Cache Memory Design
- Programmable Logic Devices
- Programmable Logic Devices
- Programmable Logic Array
- Programmable Array Logic
- Field Programmable Gate Arrays
- Digital Electronics Families
- Digital Electronics Families
- CPU Architecture
- CPU Architecture
Simplifications Using Boolean Algebra
What is a Karnaugh Map (K-Map)?
K-Map is a graphical tool used for simplifying Boolean expressions represented in their standard form to obtain their minimal form.
The K-Map is basically a graph or chart that composed of an arrangement of adjacent cells or squares, where each cell represents a particular combination of variables of the function either in sum or product form.
The number of cells in the K-Map depends upon number of variables in the Boolean function, i.e., K-map has 2n adjacent cells, where n is the number of variables in the Boolean expression. Therefore, the number of cells in a 2 variable K-map are 4 (22), in 3 variable KMap, the number of cells are 8 (23), in 4 variable K-map, the number of cells are 16 (24), and so on.
However, we can use the K Map for any number of variables. But, for simplifying Boolean functions in variables more than 5, it becomes tedious.
Now, let us discuss the procedure of simplifying a Boolean expression using K-Map.
Steps to Simplify a Boolean Expression using K Map
The following steps are involving in simplification of a given Boolean expression by using K-Map −
Step 1 − Select a K-Map as per the number of variables in the given Boolean function.
Step 2 − Identify the minterms (in SOP form) or maxterms (in POS form).
Step 3 − For SOP (Sum of Products) Form, put 1s in cells of the K-Map with respect to the minterms of given function. Read the K-Map as follows −
- Read the K-map for 1s which are not adjacent to any other 1. These 1s are the isolated minterms, thus they are to be read as they are, because they cannot be combine in groups.
- Read the K-map for 1s which are adjacent only one other 1. Combine such minterms in 2-squares.
- Read the K-map for quads (4-squares), octets (8-squares), and so on of adjacent 1s even if they have some 1s which are already combined in other groups. The only thing to remember that they must geometrically form a rectangle or a square.
- Read the K-map for any 1s that have not been grouped yet and group them into bigger squares or rectangles if possible.
- Finally, obtain product terms of all the groups, and then sum up them to form the minimal SOP expression.
For POS (Product of Sums) Form, put 0s in cells of the K-Map with respect to the maxterms of given function. Read the K-Map as follows −
- Read the K-map for 0s which are not adjacent to any other 0. These 0s are the isolated maxterms, thus they are to be read as they are, because they cannot be combine in groups.
- Read the K-map for 0s which are adjacent only one other 0. Combine such maxterms in 2-squares.
- Read the K-map for quads (4-squares), octets (8-squares), and so on of adjacent 0s even if they have some 0s which are already combined in other groups. The only thing to remember that they must geometrically form a rectangle or a square.
- Read the K-map for any 0s that have not been combined yet and combine them into bigger squares or rectangles if possible.
- Finally, obtain sum terms of all the groups, and then product them to form the minimal POS expression.
Let us understand this procedure of simplifying Boolean expression using K-map with the help of some solved examples.
Example 1
Simplify the following 3-variable Boolean function in SOP form using K-Map.
$$\mathrm{F(P, \: Q, \:R) \: = \: \sum m ( 0, \: 1, \: 3, \: 5, \: 7)}$$
Solution
The K-Map representation of the given Boolean function is shown in Figure-1.
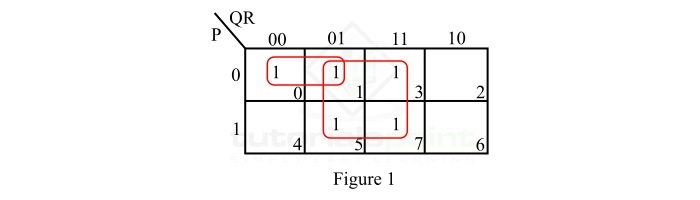
The simplification of this K-map is done as per the following steps −
- There are no isolated 1s.
- The minterm m1 forms a 4-square with minterms m3, m5, and m7. Make it and read it as R.
- The minterm m0 forms a 2-square with the minterm m1. Make it and read it as $\mathrm{\bar{P} \: \bar{Q}}$
- Write all the product terms in SOP form.
Thus, the simplified SOP expression is,
$$\mathrm{F \: = \: R \: + \: \bar{P}\bar{Q}}$$
Example 2
Simplify the following 3-variable Boolean function in POS form using K-Map.
$$\mathrm{F(A, \: B, \: C) \: = \: \Pi \: M(1, \: 2, \: 4, \: 6)}$$
Solution
The POS K-map representation of the given Boolean function is shown in Figure-2.

The simplification of this POS K-map is done as per the following steps −
- The maxterm M1 has no adjacency. Thus, keep it as it is and read it as $\mathrm{(A \: + \: B \: + \: \bar{C})}$.
- The maxterm M2 has only one adjacency M6. Hence, expand the maxterm M2 into a 2-square with the maxterm M6 and read the 2-square as $\mathrm{(\bar{B} \: + \: C)}$.
- The maxterm M4 also has only one adjacency M6. Hence, expand the maxterm M4 into a 2-square with the maxterm M6 and read the 2-square as $\mathrm{(\bar{A} \: + \: C)}$.
- Write all the sum terms in POS form.
Therefore, the simplified POS expression is,
$$\mathrm{F \: = \: (A \: + \: B \: + \: \bar{C}) \: (\bar{B} \: + \: C) \: (\bar{A} \: + \: C)}$$
Example 3
Simplify the following 4-variable Boolean function in SOP form to obtain the minimal SOP expression.
$$\mathrm{F(A, \: B, \: C, \:D) \: = \: \sum \: m( 0,\: 1, \:3, \: 5, \: 7, \: 6, \: 10, \: 13, \: 14, \: 15)}$$
Solution
SOP K-map representation of the given Boolean function is shown in Figure-3.

The simplification of this SOP K-map is done as per the following steps −
- There are no isolated 1s.
- The minterm m1 has three adjacencies m3, m5, and m7. So expand m1 into a 4-square with minterms m3, m5, and m7, and read the 4-square as $\mathrm{\bar{A}D}$.
- The minterm m5 has three adjacencies m7, m13, and m15. Expand m5 into a 4-square with minterms m7, m13, and m15, and read the 4-square as BD.
- The minterm m6 also has three adjacencies m7, m14, and m15. Expand m6 into a 4- square with minterms m7, m14, and m15, and read the 4-square as BC.
- The minterm m10 has only one adjacency m14. Expand m10 into a 2-square with minterm m14 and read the 2-square as $\mathrm{AC\bar{D}}$.
- The minterm m0 also has only one adjacency m1. Expand m0 into a 2-square with minterm m1 and read the 2-square as $\mathrm{\bar{A}\bar{B}\bar{C}}$.
- Write all the product terms in SOP form.
Hence, the simplified SOP expression is,
$$\mathrm{F \: = \: \bar{A}D \: + \: BD \: + \: BC \: + \: AC\bar{D} \: + \: \bar{A}\bar{B}\bar{C}}$$
Conclusion
In this way, we can simplify a given Boolean expression using K-map to obtain the minimal expression. Try solving the following tutorial problems for better understanding.
Q. 1 − Simplify the following 3-variable Boolean function in SOP form to obtain its minimal expression.
$$\mathrm{F(A, \: B, \: C) \: = \: \sum \: m(1, \: 2, \: 4, \: 5, \: 7)}$$
Q. 2 − Simplify the following 4-variable Boolean function in SOP form to obtain the minimal Boolean expression.
$$\mathrm{F(A, \: B, \: C, \: D) \: = \: \sum \: m(0, \: 1, \: 2, \: 4, \: 5, \: 7, \: 8, \: 9, \: 10, \: 12, \: 14, \: 15)}$$