Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Incompletely Specified Functions in Boolean Algebra
What is an Incompletely Specified Function?
In Boolean algebra, a Boolean function or logic function whose output values are known for a subset of its inputs and has output which is a don’t care condition for at least one of its input combinations is called an incompletely specified function.
Hence, in an incompletely specified function, the value of the function for don’t care combinations can be selected either a 0 or a 1 depending on the fact that which one leads to be the more minimal solution of the function. For these combinations, the Karnaugh map (K-Map) entry is marked as X which indicates that the particular cell can be taken as a 0 or a 1.
Don’t Care Combinations
Generally, we have the Boolean expressions or functions that have been completely specified for every combination of the input variables. Which means, each maxterm or minterm of the Boolean function has been specified as a 0 or a 1. But, in some cases, for certain input combinations, the value of the output is unspecified due to either the invalid input combinations or the precise value of the output is of no consequence. These combinations of input variables for which the values of the Boolean function are not specified are known as don’t care combinations. The Boolean functions having such don’t care combinations are referred to as the incompletely specified Boolean functions.
Now, let us consider the following examples to understand the incompletely specified function in more depth.
Example
Consider the following Boolean function with don’t care condition,
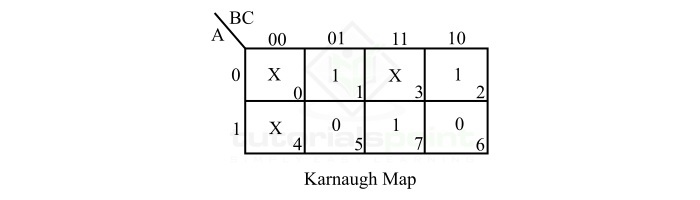
$$ F\left ( A,B,C \right )=\sum m\left ( 1,2,7 \right )+d\left ( 0,3,4 \right )$$
The truth table of this Boolean function is specified as follows −
| Inputs | Output | ||
|---|---|---|---|
| A | B | C | F |
| 0 | 0 | 0 | X |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | X |
| 1 | 0 | 0 | X |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
This function can be represented on the Karnaugh Map (K-Map) as shown in the following figure.
There are many other examples of incompletely specified Boolean functions. Like, in Excess-3 Code System, the binary combinations 0000, 0001, 0010, 1101, 1110, and 1111 are not specified and never occur in the system. Hence, these are called don’t care combinations. The logic function having these combinations or any one of these combinations is called incompletely specified function.
Another example is 8421 BCD code, in which the binary combinations 1010, 1011, 1100, 1101, 1110, and 1111 are not specified and never occur in the system. Therefore, outputs of a Boolean function corresponding to these invalid combinations are don’t cares.
Conclusion
In conclusion, a Boolean expression or logic function in which at least one combination of input variables is such that for which the output is not specified, and that combination is considered as a don’t care combination, such a Boolean function is termed as an incompletely specified logic function.
367 Views
