Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Signals and Systems – What is Quarter Wave Symmetry?
Quarter Wave Symmetry
A periodic function $x(t)$ which has either odd symmetry or even symmetry along with the half wave symmetry is said to have quarter wave symmetry.
Mathematically, a periodic function $x(t)$ is said to have quarter wave symmetry, if it satisfies the following condition −
$$\mathrm{x(t)=x(-t)\:or\:x(t)=-x(-t)\:and\:x(t)=-x\left (t ± \frac{T}{2}\right )}$$
Some examples of periodic functions having quarter wave symmetry are shown in Figure-1.
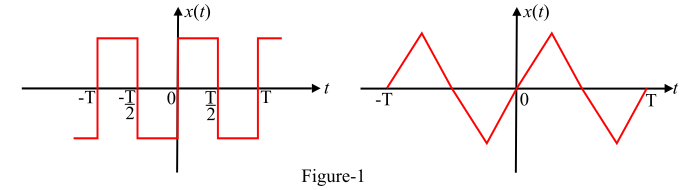
The Fourier series coefficients for the function having quarter wave symmetry are evaluated as follows −
Case I – When n is odd
$$\mathrm{x(t)=-x(-t)\:and\:x(t)=-x\left (t ± \frac{T}{2}\right )}$$
For this case,
$$\mathrm{a_{0}=0\:\:and\:\:a_{n}=0}$$
And,
$$\mathrm{b_{n}=\frac{8}{T} \int_{0}^{T/4}x(t)\:sin\:n\omega_{0}\:t\:dt}$$
Case II – When n is even
$$\mathrm{x(t)=x(-t)\:and\:x(t)=-x\left (t ± \frac{T}{2}\right )}$$
For this case,
$$\mathrm{a_{0}=0\:\:and\:\:b_{n}=0}$$
And,
$$\mathrm{a_{n}=\frac{8}{T} \int_{0}^{T/4}x(t)\:cos\:n\omega_{0}\:t\:dt}$$
Numerical Example
Find the trigonometric Fourier series for the waveform shown in Figure-2 using the quarter wave symmetry.
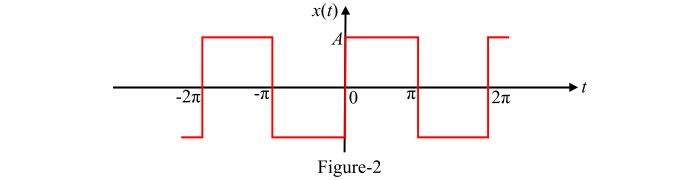
Solution
From the waveform shown in Figure-2, it is clear that it has odd symmetry along with half wave symmetry because it satisfies the following conditions −
$$\mathrm{x(t)=-x(-t)\:and\:x(t)=-x\left (t ± \frac{T}{2}\right )}$$
Therefore, the given waveform has quarter wave symmetry. Hence, the trigonometric Fourier series coefficients are,
$$\mathrm{a_{0}=0\:\:and\:\:a_{n}=0}$$
And the coefficient $b_{n}$ is given by,
$$\mathrm{b_{n}=\frac{8}{T} \int_{0}^{T/4}x(t)\:sin\:n\omega_{0}\:t\:dt}$$
Also, for this function only odd harmonics exist. Therefore,
Time period of waveform,
$$\mathrm{T= 2\pi}$$
Fundamental frequency,
$$\mathrm{\omega_{0}=\frac{2\pi}{T}=\frac{2\pi}{2\pi}=1}$$
$$\mathrm{\therefore\:b_{n}=\frac{8}{T} \int_{0}^{T/4}x(t)\:sin\:n\omega_{0}\:t\:dt=\frac{8}{2\pi}\int_{0}^{\pi/2}A\:sin\:nt\:dt}$$
$$\mathrm{\Rightarrow\:b_{n}=\frac{4A}{\pi}\left [ \frac{-cos\:nt}{n} \right ]_{0}^{\pi/2}=-\frac{4A}{n\pi}[cos(n\pi/2)-cos\:0]}$$
$$\mathrm{\therefore\:b_{n}=\begin{cases}\frac{4A}{n\pi} & for\:odd\:n\0 & for\:even\:n\end{cases}}$$
Therefore, the trigonometric Fourier series for the waveform is,
$$\mathrm{x(t)=\frac{4A}{\pi}sin\:t+\frac{4A}{3\pi}sin\:3t+\frac{4A}{5\pi}sin\:5t+....}$$
3K+ Views
