Rencontres Number (Counting partial derangements) Using C++

Given two integers N and k, we need to count the number of derangements where k points are fixed at their position. Given constraints on k are between 0 and n as the number of fixed points when there are n points cannot be more than n.

int N=4, k=2;
res = solve(N, k);

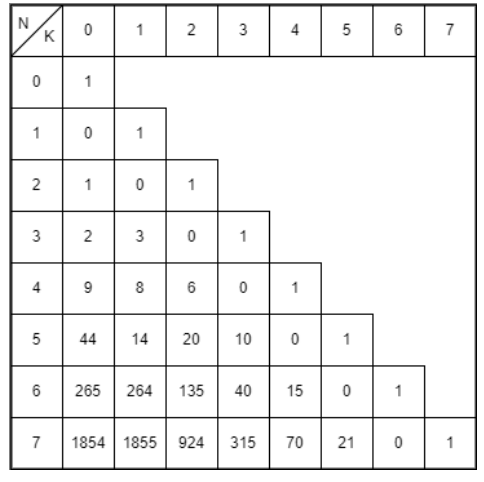
Note that at least conditions don’t hold on k. There has to be precisely and strictly k points on their original index. This is a mathematical problem. Not explaining the proof and explanation of mathematics, we as computer science majors can use the results formed by mathematicians. The result is, 𝑹𝒆𝒄𝒐𝒏𝒕𝒓𝒆𝒔(𝒏, 𝒌) = 𝒏𝑪𝒌 ∗ 𝑹𝒆𝒄𝒐𝒏𝒕𝒓𝒆𝒔(𝒏− 𝒌, 𝟎)

Let us look at some input/output scenarios

Assume the N points in which there’s no fixed points assigned, as the input. The resultant value obtained will be all the combinations of the points −

Input: N = 4, k = 0
Result: 9

We achieve 9 distinct combinations using any four coordinate points without having any fixed points.

Assume the N points in which all the points are fixed, as the input. The resultant value obtained will be all the combinations of the points −

Input: N = 4, k = 4
Result: 1

There is only one resultant combination obtained if all points are fixed.

Algorithm

The basic idea of this algorithm is derived from the idea of permutations and combinations of coordinate points on various axes. Hence, it is performed to identify the amount of ways a set of points can be plotted on a graph.

• Take number of points and the number of fixed points as an input to the method.

• We apply combination formula to find different combinations

• If there is no input, the program returns value 1.

• If there is no fixed points and one coordinate, the program returns 0.

• If there is no fixed point, the program is called recursively to find all the combinations while changing the places of all the coordinates.

• If there are fixed points, apply the combinatorial formula

Example

For example, let us consider N=3, k=1; therefore, only 1 point has to be on its original index.

If the given points are {1,3,2}, {3,2,1}, {2,1,3}, following is a C++ program to implement the Recontres number where we count the number of permutations with designated fixed points −

#include <iostream>
using namespace std;
int nCr(int n, int r) {
   if (r==0 || r==n)
      return 1;
   return nCr(n-1, r-1) + nCr(n-1, r);
}
int solve(int N, int k) {
   if (N==0 && k==0)
      return 1;
   if (N==1 && k==0)
      return 0;
   if (k==0)
      return (N-1) * (solve(N-1, 0) + solve(N-2, 0));
   return nCr(N, k) * solve(N-k, 0);
}
int main() {
   int N=3, k=1;
   cout << solve(N, k);
   return 0;
}

Output

3

Conclusion

We are using previous results to use DP to store the last values for faster processing. Also, to find the nCr, we can use an optimized approach.

Prateek Jangid

e

Updated on: 10-Aug-2022

184 Views

Kickstart Your Career

Get certified by completing the course

Get Started