Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count Derangements (Permutation such that no element appears in its original position) in C++
Derangement is permutation of N numbers such that no number appears at original position. For example one possible derangement of { 1,2,3 } is { 2,1,3 }. No element in this is at its original position. The goal here is to count the possible derangements for N numbers.
We will do this using a recursive solution. For following no. of elements −
- N=0, no derangement, return 1
- N=1, only one number, return 0
- N=2, only one swap of position possible, { 1,2 } → { 2,1 }, return 1
- N=3, 2 possible permutations eg, { 1,2,3 } → { 2,3,1 }, { 3,1,2 } count 2
- N=4, 9 possible permutations
- .......................
- N, (N-1)*( permutation(N-1) + permutation(N-2) )
For all elements in an array,
Element at index 0 has n-1 positions that it can take,
If any element at index i is placed at index 0 then, arr[i] and arr[0] are swapped. Now n-2 elements are there for calculation.
If element at index i is not placed at index 0 then for n-1 elements there are n-2 choices.
Diagram
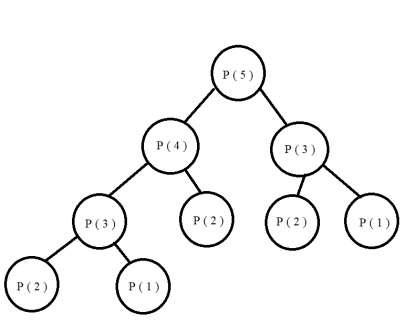
Input
Arr[] = { 1, 2 }Output
No. of derangements : 1
Explanation − Positions of 1 and 2 are index 0 and 1. Only position they can get is swapping original positions. { 2,1 }
Input
Arr[] = { 1, 2, 3 }Output
No. of derangements : 2
Explanation − Positions of 1,2 and 3 are index 0,1,2.
1 can be placed at index 1 and 2, 2 can be placed at index 0 and 3 and 3 can be placed at index 0 and 1.
{ 2,3,1 } and { 3,1,2 } are 2 derangements.
Approach used in the below program is as follows
Integer Num stores the count of numbers present.
Recursive function derangements(int N) takes the count of numbers as input and returns the no. of derangements.
The return statements for N=0,1,2 are handling the base cases for which permutations are already calculated as 1,0 and 1.
When N>2 then recursive calls to derangements() is done using the formula,
(N-1)* ( derangements ( N-1) + derangements ( N-2) ).
When backtracking starts, the count is computed and returned.
Example
#include <bits/stdc++.h>
using namespace std;
int derangements(int N){
if (N == 0)
return 1;
if (N == 1)
return 0;
if (N == 2)
return 1;
return (N - 1) * (derangements(N - 1) + derangements(N - 2));
}
int main(){
int Numbers=5;
cout<<"Number of Derangements :"<<derangements(Numbers);
}Output
Number of Derangements :44
482 Views
