Relations and Functions Worksheet

Introduction

Relation and function are the mapping between two sets. The applications of relations and functions are in every nook and corner of the real world.

In Mathematical Sciences, relations and functions are interrelated topics of study.

The examples include the conversion of base units from metres to centimetres, height and weight of a person, body temperature under different climatic conditions, Annual income for an employee's work, etc.,

If an input has only one output, then the relation is a function. The relationship of inputs and outputs in ordered pairs is a relation.

The relations and functions worksheet will provide a fundamental understanding of the concepts and help them with their real-world applications.

What are Relations?

• The input and the output values in ordered pairs of two or more non-empty sets is Relation.

• It is the connection or say, the relationship between the set elements of the provided non-empty sets.

For example,

The relation of two non-empty sets $\mathrm{A\:=\:\lbrace\:d\:,\:g\:,\:k\:,\:m\:\rbrace}$ and $\mathrm{B\:=\:\lbrace\:a\:,\:s\:,\:h\:,\:b\:\rbrace}$ is given by $\mathrm{R\:=\:\lbrace\:(d\:,\:a)\:,\:(g\:,\:s)\:,\:(k\:,\:h)\:,\:(m\:,\:b)\:,\:(g\:,\:h)\rbrace}$

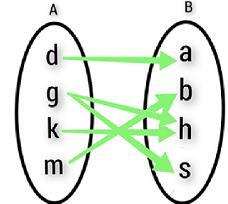
The given example is a relation but not a function since it has multiple output values for the same input.

From this mapping, we concur that the relation need not be a function in all cases.

What are the types of Relations ?

There are different types of relations, namely, Empty relations, Reflexive relations, Transitive relations, Symmetric relations, Inverse relations ,Identity relations, Universal relations and Equivalence relations.

Empty relation

If there is no mapping of the input values of a set with the values of another set then it is called the Empty relation or void relation.

$$\mathrm{R\:=\:\phi}$$

Reflexive relation

If the elements of set A are mapped to itself then the relation is called Reflexive relation.

Transitive relation

A relation is said to be Transitive if $\mathrm{pRq\:and\:qRr\:\Longrightarrow\:pRr}$

Symmetric relation

Symmetric relation contains the ordered pair of a set and its reversed ordered pair.

Inverse relation

If a set contains the inverse pairs of another set then that type of relation is called Inverse relation.

Identity relation

A relation is said to be Identity relation if all elements in a set A are mapped to itself.

Universal relation

If all the elements of one set are mapped to the other set elements or the set itself then that type of relation is called Universal relation.

Equivalence Relation

If a relation is symmetric, transitive and reflexive we call that relation an Equivalence relation.

What are Functions?

In a relation if each input value is assigned to a distinct output value then the relation is said to be a Function

• The domain of a function is the set of all inputs for a function

• The Co-domain of a function is the set of elements that may possibly become the outputs of a function.

• The Range of a function is the output values of the function.

For Example

Let the two non-empty sets be {2, 3, 5 } and {3, 4, 6, 7, 8 }. If the relation 𝑅 ={(2, 3), (3, 4), (5, 6)}. What will be the domain, co-domain and the range?

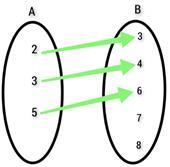
Answer −

The domain of the function = {2, 3, 5 }

The co-domain of the function = {3, 4, 6, 7, 8 }

The range of the function = {3, 4, 6}

What are the types of Functions?

There are various kinds of mapping, namely, One to One Function, Onto function, and Into function.

One to One Function

If for every input value there is a distinct output value then that type of function is called a one to one function

Onto function

If for every output value there is definitely a value in another set then it is called Onto function or surjective function.

Into function

If at least one element in the co-domain set is not mapped by any element of the domain set then the function is said to be Into function

Solved Examples

1) Let $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ be a function defined by $\mathrm{f(x)\:=\:x^{2}\:+\:1}$ where 𝒙 takes the values 0,1,2 and 3. Find the range of the function.

Answer −

By substituting the given input values in $\mathrm{f(x)\:=\:x^{2}\:+\:1}$ , we get

$\mathrm{f(0)\:=\:1\:,\:f(1)\:=\:2\:,\:f(2)\:=\:5\:and\:f(3)\:=\:10}$

The Range of the function = {1, 2, 5, 10}

2) From the given mapping diagram, find the domain and the range of the function.

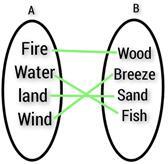
Answer −

The domain set $\mathrm{=\:\lbrace\:Fire\:,\:Water\:,\:Land\:,\:Wind\:\rbrace}$

The range set $\mathrm{=\:\lbrace\:Wood\:,\:Breeze\:,\:Sand\:,\:Fish\:\rbrace}$

3) Let the two non-empty sets be $\mathrm{A\:=\:\lbrace\:7\:,\:8\:,\:9\:,\:10\:\rbrace}$ and $\mathrm{B\:=\:\lbrace\:1\:,\:2\:,\:3\:,\:4\:\rbrace}$. If a function $\mathrm{f(x)}$ is defined from A to B then what will be the input and output values of the function?

Answer −

The input values will be the set $\mathrm{A\:=\:\lbrace\:7\:,\:8\:,\:9\:,\:10\:\rbrace}$

The output values will be the set $\mathrm{B\:=\:\lbrace\:1\:,\:2\:,\:3\:,\:4\:\rbrace}$

4) Find the domain, co-domain and the range of the function from the given mapping diagram

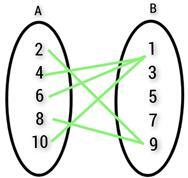
Answer −

The domain set = {2,4,6,8,10}

The co-domain set= {1,3,5,7,9}

The range set = {1, 9}

5) The function F from A to B is defined by $\mathrm{\lbrace\:(1\:,\:b)\:,\:(3\:,\:e)\:,\:(7\:,\:m)\:,\:(9\:,\:u)\:\rbrace}$. Draw the mapping diagram for this function and mention its type.

Answer −

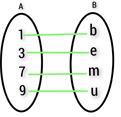
The above mapping is a one-to-one function.

6) Let $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ be a function such that $\mathrm{f(x)\:=\:\lbrace\:(4\:,\:6)\:,\:(7\:,\:9)\:,\:(8\:,\:9)\:\rbrace}$. Find the type of function with the help of a mapping diagram.

Answer −

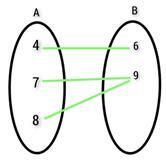
The type of the given function is onto.

7) If the domain of the function be {𝟐, 𝟓, 𝟗 } and the range be {𝟐, 𝟓, 𝟗 }. What is this type of relation called and is it a function?

Answer − If every element is related to itself then the relation is Reflexive. Yes, this type of relation is a Function

8) Suppose the function is defined by $\mathrm{f(x)\:=\:\lbrace\:(1\:,\:1)\:,\:(2\:,\:2)\:,\:(3\:,\:3)\:,\:(4\:,\:4)\:\rbrace}$ .what type of relation is this function?

Answer −

In the given function

$\mathrm{f(x)\:=\:\lbrace\:(1\:,\:1)\:,\:(2\:,\:2)\:,\:(3\:,\:3)\:,\:(4\:,\:4)\:\rbrace}$ the type of relation is identity relation. Since all the elements in a set are mapped to itself

9) If the range of a function is $\mathrm{\lbrace\:e\:,\:r\:,\:f\:,\:g\:,\:h\:\rbrace}$. What will be the defined function?

Answer − The given data is insufficient. Without knowing the domain the given range value will be invalid and it is not possible to find the type of relation or the function

10) If the Set $\mathrm{A\:=\:\lbrace\:W\:,\:X\:,\:Y\:,\:Z\:\rbrace}$ and Set $\mathrm{B\:=\:\lbrace\:A\:,\:B\:,\:C\:,\:D\:\rbrace}$ and the defined function F from A to B is $\mathrm{f(x)\:=\:\lbrace\:(W\:,\:C)\:,\:(X\:,\:D)\:,\:(Y\:,\:B)\:,\:(Z\:,\:A)\:\rbrace}$. Map the given function. S

Answer −

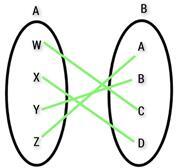
11) From the given mapping diagram, find the defined function F from A to B.

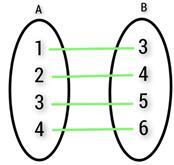
Answer − The function defined from A to B is {(1,2), (2,4), (3,5), (4,6)}

12) From the given mapping diagram, find the non-empty sets.

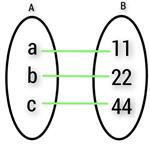
Solution − The non-empty sets are $\mathrm{A\:=\:\lbrace\:a\:,\:b\:,\:c\:\rbrace}$ and $\mathrm{B\:=\:\lbrace\:11\:,\:22\:,\:44\:\rbrace}$

Problems For Practice

• Suppose the function is defined by $\mathrm{f(x)\:=\:\lbrace\:(a\:,\:a)\:,\:(b\:,\:b)\:,\:(c\:,\:c)\:,\:(d\:,\:a)\:\rbrace}$ .what type of relation is this function?

• Let $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ be a function defined by $\mathrm{f(x)\:=\:2x^{3}\:+\:1}$ where 𝑥 takes the values 1,2, 3 and 4. Find the range of the function

• The function F from A to B is defined by $\mathrm{\lbrace\:(F\:,\:D)\:,\:(Y\:,\:D)\:,\:(U\:,\:P)\:,\:(S\:,\:Q)\:\rbrace}$. Draw the mapping diagram for this function and mention its type.

• From the given mapping diagram, find the defined function F from A to B.

• Let $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ be a function defined by $\mathrm{f(x)\:=\:x\:+\:5}$ for every 𝑥 > 0, draw a mapping diagram for the defined function

• If a relation is defined by $\mathrm{R\:=\:\lbrace\:(9\:,\:0)\:,\:(2\:,\:5)\:,\:(7\:,\:8)\:,\:(7\:,\:4)\:\rbrace}$ . Is R a function?

• If a function $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ is defined by 𝑓(𝑥) = {(e,p), (l,b), (s,f),(k,q)}. Find the domain and the range of the function.

Conclusion

• A relation is a set of ordered pairs that defines the connection between the elements of two or more sets.

• A function is a relationship where every input has a unique output

• The input values are the domain of the function

• Range is a part or the subset of the Co- domain

• In order to find the type of function, we should map the values from domain to co- domain.

FAQs

1. What are preimage and image in a function?

• The set of elements that map to a given set of elements is called pre-images. It is a subset of co-domain.

• The set of all output values the function may produce is called the image of the function. It is a subset of the domain

2. When is a relation not a function?

If a single input value has two or more outputs, that type of one-to-many mapping is not a function

For example $\mathrm{R\:=\:\lbrace\:(a\:,\:n)\:,\:(e\:,\:t)\:,\:(a\:,\:v)\:,\:(m\:,\:g)\rbrace}$

3. What is a vertical line test?

If the curve of the function intersects the vertical line we draw on the XYplane more than once, it is not a function, but if the vertical line intersects at one point, then it is a function. This is one of the visual ways to determine whether the function has one output value or more than one

4. What is a Bijective Function?

If a function is a one-to-one and onto, then that function is said to be a Bijective function

5. What type of function is called an injective function?

If a function is a one-to-one then that function is said to be an injective function.