Relations and Functions

Introduction

A relation is defined as the mutual dependence of one element on another. In mathematics, the function represents the specific relationships between two sets of elements. In this tutorial, we will discuss the meaning of relations and functions, their various types, and the inverse of a function with solved examples.

Relations

The relation is a binary relation between two classes or sets, representing that the elements of both classes are somehow related. The binary relation between two sets X and Y is a set of ordered pairs of elements, i.e., (x, y), in such a way that the element x belongs to the set X and the element y belongs to the set Y. The relation is denoted by a symbol R. It contains the ordered pair of elements of both sets.

Mathematically, the binary relation can be expressed as

$$\mathrm{X\:\times\:Y\:=\:=\:\lbrace(x\:,\:y)\:\lvert\:x\:\varepsilon\:X\:and\:y\:\varepsilon\:Y\rbrace}$$

Here X is known as the domain for R and Y is called the range for R. The relation in mathematics can be represented in three ways.

• Roster form − In this type of presentation, the relation is usually expressed in the form of ordered pairs of the elements.

For example, $\mathrm{set\:A\:=\:\lbrace\:-1\:,\:4\:,\:0\:,\:8\:\rbrace\:,\:B\:=\:\lbrace\:-2\:,\:-11\:,\:4\:,\:-2\:\rbrace}$

Now the relation between the two sets can be represented as

$\mathrm{R\:\colon\:A\:\rightarrow\:B\:=\:\lbrace\:(-1\:,\:-2)\:,\:(4\:,\:-11)\:,\:(0\:,\:4)\:,\:(8\:-2)\rbrace\:}$

• Set-builder form − This is used to express a large number of elements in a short form. It is used to describe the relationship between the sets with the help of an equation or interval.

For example, $\mathrm{\lbrace\:3\:,\:6\:,\:9\:,\:12\:,\:15\:,\:18\:,\:21\:\rbrace\:}$

Now, it can be expressed as

$\mathrm{\lbrace\:p\:\colon\:p\:=\:3n\:,\:n\:\varepsilon\:N\:,\:1\:\leq\:n\:\leq\:7\:\rbrace\:}$

• By arrow diagram − In this method, the relation between the individual elements of one set to another is presented by drawing arrows directed from left to right.

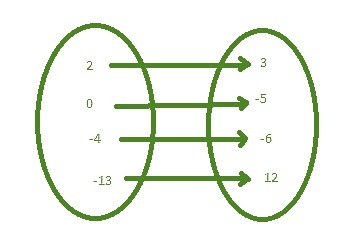
For example − $\mathrm{set\:A\:=\:\lbrace\:2\:,\:0\:,\:-4\:,\:-13\:\rbrace\:,\:B\:=\:3\:,\:-5\:,\:-6\:,\:12\:\rbrace\:}$

Now the relation between the two sets can be represented as

$\mathrm{R\:\colon\:A\:\rightarrow\:B\:=\:\lbrace\:(2\:,\:3)\:,\:(0\:,\:-5)\:,\:(-4\:,\:-6)\:,\:(-13\:,\:12)\:\rbrace\:}$

Types of Relations

In mathematics, various types of relations are used. Each type of relation is briefly mentioned below.

• Reflexive

• Symmetric

• Transitive

• Equivalence

Let's discuss each type of relation in detail.

Reflexive

R is called reflexive if $\mathrm{(p\:,\:p)\:\varepsilon\:R\:,\:for\:every\:p\:\varepsilon\:A}$.

Symmetric

R is called symmetric if and only $\mathrm{(p\:,\:q\:)\:\varepsilon\:R\:,\:then\:(q\:,\:p)\:\varepsilon\:R}$.

Transitive

R is called symmetric if and only $\mathrm{(p\:,\:q\:)\varepsilon\:R\:and\:(q\:,\:r)\varepsilon\:R\:,\:then\:(p\:,\:r)\varepsilon\:R}$.

Equivalence

R is called equivalence if it is reflective, symmetric, and transitive.

Functions

A function from a set A to B is an assignment of an element of B to each element of A. In other words, a relation R from set A to B is said to be a function if each element of A has one and only one image in set B.

Types of Functions

In mathematics, various functions are studied, which are mentioned below.

• One-one and many-one

• Onto and into

• Bijective

Let’s discuss each type of function in detail.

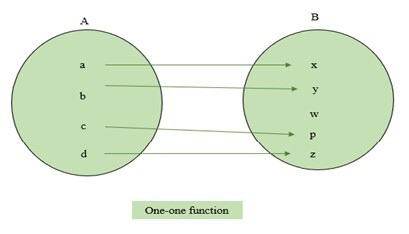
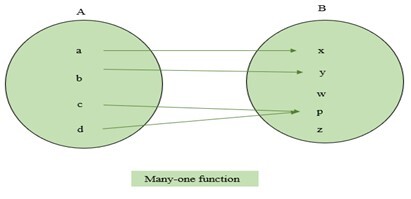
One-one and Many-one

A function $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ is called a one-one function if the mapping of each element of set A to the element of set B is distinct. It is also called the injective function. If any element of set A is mapped with multiple elements of B, it is called a many- one function. The examples of one-one and many-one functions are represented below.

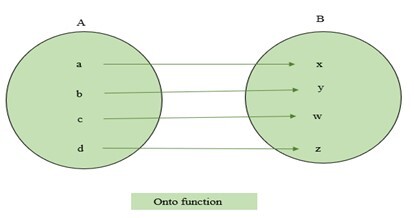
Onto and Into

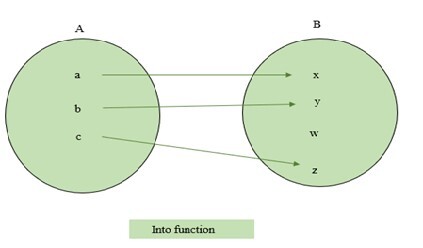
A function $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ is called an onto function if each element of B is the image of some element of A under 𝑓. In other words, if the range of the function becomes B, then it is known as an onto function. The into function is the reverse of onto. That means, if one element of B is not the image of some element of A, it is called an into function. The examples of one-one and many-one functions are represented below.

Bijective

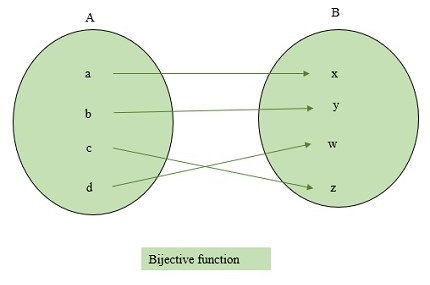
If a function is both one-one and onto function, it is called a bijective function.

Composition of Functions

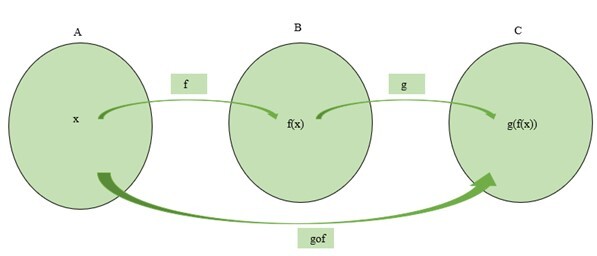
In mathematics, two functions say f and g produce a new function j (say) so that,

$\mathrm{f(x)\:=\:g(f(x))}$.

Let’s consider a function $\mathrm{f\:\colon\:A\:\rightarrow\:B}$ and $\mathrm{g\:\colon\:B\:\rightarrow\:C}$ are two functions. The composition of the above functions can be written as $\mathrm{gof\:\colon\:A\:\rightarrow\:C\:and\:gof\:=\:g(f(x))}$ The schematic representation of composition of functions is illustrated below.

Inverse of a Function

A function $\mathrm{g\:\colon\:B\:\rightarrow\:C}$ is said to be the inverse of function $\mathrm{f\:\colon\:C\:\rightarrow\:B}$, if $\mathrm{gof\:=\:I_{C}\:and\:fog\:=\:I_{B}}$. If an inverse function exists of a function, then it is called an invertible function. It is to be noted that an invertible function is a bijective function.

Solved Examples

Example 1

Let’s consider a set $\mathrm{P\:=\:\lbrace\:-7\:,\:5\:,\:-6\:,\:3\:\rbrace\:}$ and the relation is given by $\mathrm{R\:=\:\lbrace\:(-7\:,\:5)\:,\:(-7\:,\:7)\:,\:(5\:,\:5)\:,\:(-6\:,\:3)\:,\:(3\:,\:3)\:,\:(-6\:,\:-6)\:,\:\rbrace\:}$ Check weather the relation is an equivalent relation or not.

Solution −

Reflexive property − The relation R is reflexive since $\mathrm{(-7\:,\:-7)\:,\:(5\:,\:5)\:,\:(-6\:,\:-6)\:,\:(3\:,\:3)\:R}$.

Symmetric property − The relation R is not symmetric since $\mathrm{(p\:,\:q)\:R\:,\:but\:(q\:,\:p)}$ For example $\mathrm{(-7\:,\:5)R\:,\:but\:(5\:,\:7)R}$

Transitive property − The relation R is transitive since $\mathrm{(p\:,\:q)R\:,\:but\:(p\:,\:r)\:R}$

∴ The above relation is reflexive and transitive. However, it doesn't satisfy the symmetric property. Hence, the above relation is not an equivalence relation.

Example 2:

If $\mathrm{f(x)\:=\:3x\:and\:g(x)\:=\:5x\:-\:8}$ then evaluate fog.

Solution −

It is given that,

$\mathrm{f(x)\:=\:3x\:and\:g(x)\:=\:5x\:-\:8}$

$\mathrm{fog\:=\:f(g(x))\:=\:f(5x\:-\:8)}$

Now putting the value of $\mathrm{x\:=\:5x\:-\:8\:in\:f(x)}$ we get

$\mathrm{\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:fog\:=\:3(5x\:-\:8)\:=\:15x\:-\:24}$

Conclusion

The present article gives a brief idea about the relations and functions. The definitions and their various types have been described in this article. In addition, some solved examples have been provided for better clarity of this concept. In conclusion, the present article may be useful for understanding the basic concept of relations and functions.

FAQs

1. All relations are functions. Is the statement true?

No. All functions are relations. However, the reverse may not be true.

2. What do you mean by identity function?

A function is said to be an identity function if each element of set B gives the image itself as the same element.

3. What is the basic difference between relation and function?

A relation may have multiple outputs for an input. However, a function has a single output for an input. All the functions can be called relations. But, the reverse may not be true.

4. Give some real-life examples of relations?

The real-life examples of relations are

• The number of calories in one energy drink.

• Distance covered with 6.0 litre of diesel in the tank.

5. What do you mean by domain in a relation?

The set containing all the first elements of the relation is known as domain.