Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Rational numbers (fractions)
Any number which can be expressed as a quotient or fraction in the form of p/q is called a rational number. The fractions module of Python library provides functionality for rational number arithmetic.
This module defines a Fraction class. Its object can be constituted in various ways as below −
Fraction(num, denom)
The first version of Fraction constructor receives two parameters for numerator and denominator. Default numerator is 0 and default denominator is 1. Value of denominator = 0 throws ZeroDivisionError.
>>> from fractions import Fraction >>> n1 = Fraction(2,5) >>> n1 Fraction(2, 5) >>> n2 = Fraction(6,15) >>> n2 Fraction(2, 5) >>> n3 = Fraction(10,1) >>> n3 Fraction(10, 1) >>> n3 = Fraction(10) >>> n3 Fraction(10, 1)
Note that numerator and denominator parameters are reduced to minimum values after dividing them by common factors.
Fraction constructor can also receive string parameter provided it contains valid numeric representation.
>>> n1 = Fraction('5')
>>> n1
Fraction(5, 1)
>>> n2 = Fraction('4/7')
>>> n2
Fraction(4, 7)
>>> n3 = Fraction('0.25')
>>> n3
Fraction(1, 4)
>>> n4 = Fraction('1.23E4')
>>> n4
Fraction(12300, 1)A floating point number can also be a parameter to the constructor. However, because of the representation of float in pure binary form, the quotient of numerator and denominator of resultant Fraction object may not be exact. On the other hand, an object of the Decimal class as a parameter also produces a Fraction object.
>>> from fractions import Fraction
>>> from decimal import Decimal
>>> n1 = Fraction(2.1)
>>> n1
Fraction(4728779608739021, 2251799813685248)
>>> n2 = Fraction(Decimal('2.1'))
>>> n2
Fraction(21, 10)All arithmetic operations are permissible with Fraction objects.
>>> n1 = Fraction(2,3) >>> n2 = Fraction(1,2) >>> n1+n2 Fraction(7, 6) >>> n1-n2 Fraction(1, 6) >>> n1*n2 Fraction(1, 3) >>> n1/n2 Fraction(4, 3)
Just to recall how random number arithmetic is performed in quotient form −
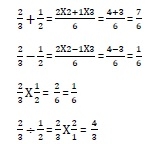
Fraction object has two attributes, numerator and denominator which can be accessed independently.
>>> n1 = Fraction(2,3) >>> n1.numerator 2 >>> n1.denominator 3
The Fraction class has following useful methods to find the largest integer smaller than quotient (floor value) and a smallest integer greater than quotient (ceil value)
>>> n1 = Fraction(355,113) >>> n1.__floor__() 3 >>> n1.__ceil__() 4
Another class method limit_denominator() returns the closest fraction that has denominator at the most equal to the specified value.
>>> Fraction('2.71828').limit_denominator(400)
Fraction(1071, 394)In this article features and function in the fractions module of the Python standard library have been discussed.
2K+ Views
