Python Program for 0-1 Knapsack Problem

In this article, we will learn about the solution to the problem statement given below.

Problem statement − We are given weights and values of n items, we need to put these items in a bag of capacity W up to the maximum capacity w. We need to carry a maximum number of items and return its value.

Now let’s observe the solution in the implementation below −

# Brute-force approach

Example

 Live Demo

#Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   # initial conditions
   if n == 0 or W == 0 :
      return 0
   # If weight is higher than capacity then it is not included
   if (wt[n-1] > W):
      return knapSack(W, wt, val, n-1)
   # return either nth item being included or not
   else:
      return max(val[n-1] + knapSack(W-wt[n-1], wt, val, n-1),
         knapSack(W, wt, val, n-1))
# To test above function
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print (knapSack(W, wt, val, n))

Output

350

#dynamic approach

Example

 Live Demo

# a dynamic approach
# Returns the maximum value that can be stored by the bag
def knapSack(W, wt, val, n):
   K = [[0 for x in range(W + 1)] for x in range(n + 1)]
   #Table in bottom up manner
   for i in range(n + 1):
      for w in range(W + 1):
         if i == 0 or w == 0:
            K[i][w] = 0
         elif wt[i-1] <= w:
            K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
         else:
            K[i][w] = K[i-1][w]
   return K[n][W]
#Main
val = [50,100,150,200]
wt = [8,16,32,40]
W = 64
n = len(val)
print(knapSack(W, wt, val, n))

Output

350

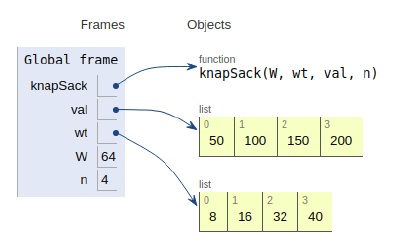
All the variables are declared in the local scope and their references are seen in the figure above.

Conclusion

In this article, we have learned about how we can make a Python Program for 0-1 Knapsack Problem

Updated on: 20-Dec-2019

5K+ Views

Kickstart Your Career

Get certified by completing the course

Get Started
Advertisements