
- ML - Home
- ML - Introduction
- ML - Getting Started
- ML - Basic Concepts
- ML - Ecosystem
- ML - Python Libraries
- ML - Applications
- ML - Life Cycle
- ML - Required Skills
- ML - Implementation
- ML - Challenges & Common Issues
- ML - Limitations
- ML - Reallife Examples
- ML - Data Structure
- ML - Mathematics
- ML - Artificial Intelligence
- ML - Neural Networks
- ML - Deep Learning
- ML - Getting Datasets
- ML - Categorical Data
- ML - Data Loading
- ML - Data Understanding
- ML - Data Preparation
- ML - Models
- ML - Supervised Learning
- ML - Unsupervised Learning
- ML - Semi-supervised Learning
- ML - Reinforcement Learning
- ML - Supervised vs. Unsupervised
Machine Learning Data Visualization
- ML - Data Visualization
- ML - Histograms
- ML - Density Plots
- ML - Box and Whisker Plots
- ML - Correlation Matrix Plots
- ML - Scatter Matrix Plots
Statistics for Machine Learning
- ML - Statistics
- ML - Mean, Median, Mode
- ML - Standard Deviation
- ML - Percentiles
- ML - Data Distribution
- ML - Skewness and Kurtosis
- ML - Bias and Variance
- ML - Hypothesis
Regression Analysis In ML
- ML - Regression Analysis
- ML - Linear Regression
- ML - Simple Linear Regression
- ML - Multiple Linear Regression
- ML - Polynomial Regression
- ML - Classification Algorithms
- ML - Logistic Regression
- ML - K-Nearest Neighbors (KNN)
- ML - Naïve Bayes Algorithm
- ML - Decision Tree Algorithm
- ML - Support Vector Machine
- ML - Random Forest
- ML - Confusion Matrix
- ML - Stochastic Gradient Descent
- ML - Clustering Algorithms
- ML - Centroid-Based Clustering
- ML - K-Means Clustering
- ML - K-Medoids Clustering
- ML - Mean-Shift Clustering
- ML - Hierarchical Clustering
- ML - Density-Based Clustering
- ML - DBSCAN Clustering
- ML - OPTICS Clustering
- ML - HDBSCAN Clustering
- ML - BIRCH Clustering
- ML - Affinity Propagation
- ML - Distribution-Based Clustering
- ML - Agglomerative Clustering
- ML - Dimensionality Reduction
- ML - Feature Selection
- ML - Feature Extraction
- ML - Backward Elimination
- ML - Forward Feature Construction
- ML - High Correlation Filter
- ML - Low Variance Filter
- ML - Missing Values Ratio
- ML - Principal Component Analysis
- ML - Reinforcement Learning Algorithms
- ML - Exploitation & Exploration
- ML - Q-Learning
- ML - REINFORCE Algorithm
- ML - SARSA Reinforcement Learning
- ML - Actor-critic Method
- ML - Monte Carlo Methods
- ML - Temporal Difference
- ML - Deep Reinforcement Learning
- ML - Deep Reinforcement Learning Algorithms
- ML - Deep Q-Networks
- ML - Deep Deterministic Policy Gradient
- ML - Trust Region Methods
- ML - Performance Metrics
- ML - Automatic Workflows
- ML - Boost Model Performance
- ML - Gradient Boosting
- ML - Bootstrap Aggregation (Bagging)
- ML - Cross Validation
- ML - AUC-ROC Curve
- ML - Grid Search
- ML - Data Scaling
- ML - Train and Test
- ML - Association Rules
- ML - Apriori Algorithm
- ML - Gaussian Discriminant Analysis
- ML - Cost Function
- ML - Bayes Theorem
- ML - Precision and Recall
- ML - Adversarial
- ML - Stacking
- ML - Epoch
- ML - Perceptron
- ML - Regularization
- ML - Overfitting
- ML - P-value
- ML - Entropy
- ML - MLOps
- ML - Data Leakage
- ML - Monetizing Machine Learning
- ML - Types of Data
Classification Algorithms In ML
Clustering Algorithms In ML
Dimensionality Reduction In ML
Reinforcement Learning
Deep Reinforcement Learning
Quantum Machine Learning
Machine Learning Miscellaneous
Machine Learning - Resources
Polynomial Regression in Machine Learning
What is Polynomial Regression?
Polynomial Linear Regression is a type of regression analysis in which the relationship between the independent variable and the dependent variable is modeled as an n-th degree polynomial function. Polynomial regression allows for a more complex relationship between the variables to be captured beyond the linear relationship in simple linear regression and multiple linear regression.
Why Polynomial Regression?
In machine learning (ML) and data science, choosing between a linear regression or polynomial regression depends upon the characteristics of the dataset. A non-linear dataset can't be fitted with a linear regression. If we apply linear regression to a nonlinear dataset, it will not be able to capture the non-linear patterns in the data.
Look at the below diagram to understand why we need polynomial regression for non-linear data.
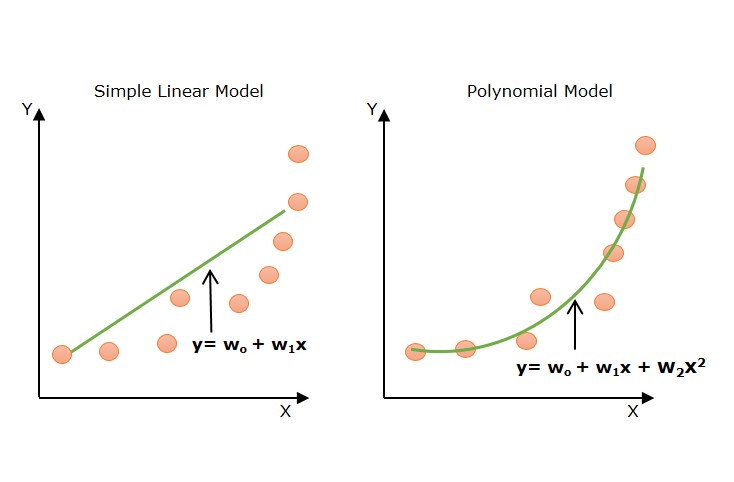
The above diagram shows the simple linear model hardly fits the data points whereas the polynomial model fits most of the data points.
Equation of Polynomial Regression Model
In machine learning, the general formula for polynomial regression of degree ${n}$ is as follows −
$$\mathrm{y \: = \: w_{0} \: + \:w_1 x \:+ \: w_2 x^2 \: + \: w_{3} x^3 \: + \: \dotso\: + \: w_n x^n \: + \: \epsilon}$$
Where
- ${y}$ is the dependent variable (output).
- ${x}$ is the independent variable (input).
- ${w_{0}, w_{1}, w_{2}, \dots, w_{n}}$ are the coefficients (parameters) of the model.
- ${n}$ is the degree of the polynomial (the highest power of ${x}$).
- ${\epsilon}$ is the error term or residual, representing the difference between the observed value and the model's prediction.
For a quadratic (second-degree) polynomial regression, the formula would be:
$$\mathrm{y \:=\: w_{0} \:+\: w_{1} x \:+\: w_{2} x^2 \:+\: \epsilon}$$
This would fit a parabolic curve to the data points.
How does Polynomial Regression Work?
In machine learning, the polynomial regression actually works in a similar way as linear regression works. It is modeled as multiple linear regression. The input feature is transformed into polynomial features of higher degrees (${x^2, x^3, ..., x^n}$). These features are now treated as separate independent variables as in multiple linear regression. Now, a multiple linear regressor is trained on these transformed polynomial features.
The polynomial regression is a special case of multiple linear regression but there is a difference that multiple linear regression assumes linearity of input features. Here, in polynomial regression, the transformed polynomial features are dependent on the original input feature.
Implementation of Polynomial Regression using Python
Let's implement polynomial regression using Python. We will use a well known machine learning Python library, Scikit-learn for building a regression model.
Step 1: Data Preparation
In machine learning model building, the data preparation is very important step. Let's prepare our data first. We will be using a dataset named ice_cream_selling_data.csv. It contains 49 data examples. It has an input feature/ independent variable (Temperature (C)) and target feature/ dependent variable (Ice Cream Sales (units)).
The following table represents the data in ice_cream_selling_data.csv file.
ice_cream_selling_data.csv
| Temperature (C) | Ice Cream Sales (units) |
|---|---|
| -4.662262677 | 41.84298632 |
| -4.316559447 | 34.66111954 |
| -4.213984765 | 39.38300088 |
| -3.949661089 | 37.53984488 |
| -3.578553716 | 32.28453119 |
| -3.455711698 | 30.00113848 |
| -3.108440121 | 22.63540128 |
| -3.081303324 | 25.36502221 |
| -2.672460827 | 19.22697005 |
| -2.652286793 | 20.27967918 |
| -2.651498033 | 13.2758285 |
| -2.288263998 | 18.12399121 |
| -2.11186969 | 11.21829447 |
| -1.818937609 | 10.01286785 |
| -1.66034773 | 12.61518115 |
| -1.326378983 | 10.95773134 |
| -1.173123268 | 6.68912264 |
| -0.773330043 | 9.392968661 |
| -0.673752802 | 5.210162615 |
| -0.149634867 | 4.673642541 |
| -0.036156498 | 0.328625517 |
| -0.033895286 | 0.897603187 |
| 0.008607699 | 3.165600008 |
| 0.149244574 | 1.931416029 |
| 0.688780908 | 2.576782245 |
| 0.693598873 | 4.625689458 |
| 0.874905029 | 0.789973651 |
| 1.024180814 | 2.313806358 |
| 1.240711619 | 1.292360811 |
| 1.359812674 | 0.953115312 |
| 1.740000012 | 3.782570136 |
| 1.850551926 | 4.857987801 |
| 1.999310369 | 8.943823209 |
| 2.075100597 | 8.170734936 |
| 2.31859124 | 7.412094028 |
| 2.471945997 | 10.33663062 |
| 2.784836463 | 15.99661997 |
| 2.831760211 | 12.56823739 |
| 2.959932091 | 21.34291574 |
| 3.020874314 | 20.11441346 |
| 3.211366144 | 22.8394055 |
| 3.270044068 | 16.98327874 |
| 3.316072519 | 25.14208223 |
| 3.335932412 | 26.10474041 |
| 3.610778478 | 28.91218793 |
| 3.704057438 | 17.84395652 |
| 4.130867961 | 34.53074274 |
| 4.133533788 | 27.69838335 |
| 4.899031514 | 41.51482194 |
Note − Create a CSV file with the above data and save it as ice_cream_selling_data.csv.
Import Python libraries and packages for data preparation
Let's first import libraries and packages required in the data preparation step. We use Python pandas for reading CSV files. We use NumPy to convert the pandas data frame to NumPy array. Input and output features are NumPy arrays. We use preprocessing package from the Scikit-learn library for preprocessing related tasks such as transforming input feature to polynomial features.
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures
Load the dataset
Load the ice_cream_selling_data.csv as a pandas dataframe. Learn more about data loading here.
data = pd.read_csv('/ice_cream_selling_data.csv')
data.head()
Output
Temperature (C) Ice Cream Sales (units) 0 -4.662263 41.842986 1 -4.316559 34.661120 2 -4.213985 39.383001 3 -3.949661 37.539845 4 -3.578554 32.284531
Let's create independent variable (${X}$) and the dependent variable (${y}$).
X = data.iloc[:, 0].values.reshape(-1, 1) y = data.iloc[:, 1].values
Visualize the original datapoints
Let's visualize the original data points to get some insight.
# Visualize the original data points
plt.scatter(X, y, color="green")
plt.title("Original Data")
plt.xlabel("Temperature (C)")
plt.ylabel("Ice Cream Sales (units)")
plt.show()
Output
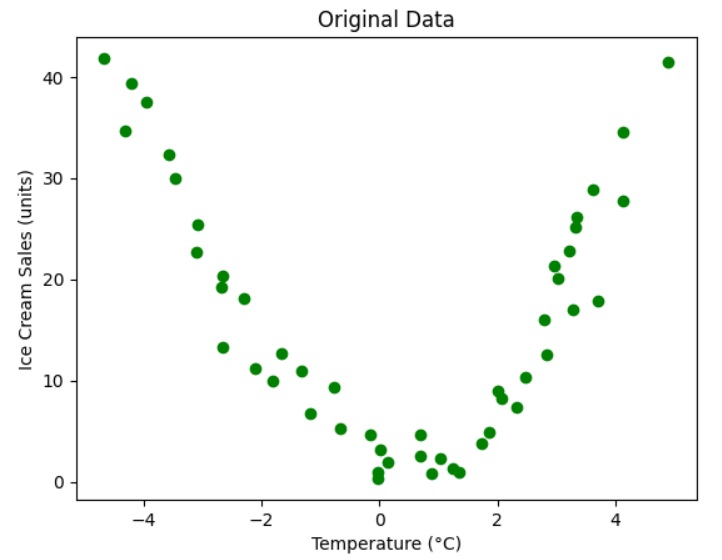
The above graph shows a parabolic curve (polynomial with degree 2) that will fit the datapoints.
So the relationship between the dependent variable ("Ice Cream Sales (units)") and independent variable ("Temperature (C)") can be modeled using polynomial regression of degree 2.
Create a polynomial features object
Now, let's create a polynomial feature object with degree 2. We will use PolynomialFeatures class from sklearn.preprocessing module to create the feature object.
degree = 2 # Degree of the polynomial poly_features = PolynomialFeatures(degree=degree)
Let's now transform the input data to include polynomial features
X_poly = poly_features.fit_transform(X)
Here ${X\_poly}$ is transformed polynomial features of original input features (${X}$). The transformed data is of (49, 3) shape.
Step 2: Model Training
We have created polynomial features. Now, let's build out the model. We use LinearRegression class from sklearn.linear_model module. As we already discussed, Polynomial regression is a special type of linear regression.
Let's create a linear regression object lr_model and train (fit) the model with data.
from sklearn.linear_model import LinearRegression lr_model = LinearRegression() #Now, fit the model (linear regression object) on the data lr_model.fit(X_poly, y)
So far, we have trained our regression model lr_model
Step 3: Model Prediction and Testing
Now, we can use our model to predict the output. Before going to predict for new data, let's predict for the existing data.
# Generate predictions
y_pred = lr_model.predict(X_poly)
df = pd.DataFrame({'Actual Values':y, 'Predicted Values':y_pred})
print(df)
Output
Actual Values Predicted Values
0 41.842986 46.564507
1 34.661120 40.600548
2 39.383001 38.915089
3 37.539845 34.749272
4 32.284531 29.331940
5 30.001138 27.649735
6 22.635401 23.192862
7 25.365022 22.863178
8 19.226970 18.222266
9 20.279679 18.009098
10 13.275828 18.000794
11 18.123991 14.418541
12 11.218294 12.853070
13 10.012868 10.504868
14 12.615181 9.364587
15 10.957731 7.264266
16 6.689123 6.437055
17 9.392969 4.683654
18 5.210163 4.337906
19 4.673643 3.116139
20 0.328626 2.983983
21 0.897603 2.981829
22 3.165600 2.944811
23 1.931416 2.869446
24 2.576782 3.251711
25 4.625689 3.259923
26 0.789974 3.630683
27 2.313806 4.026226
28 1.292361 4.744891
29 0.953115 5.213321
30 3.782570 7.055902
31 4.857988 7.690948
32 8.943823 8.616039
33 8.170735 9.118494
34 7.412094 10.874961
35 10.336631 12.092557
36 15.996620 14.843721
37 12.568237 15.287199
38 21.342916 16.539614
39 20.114413 17.156188
40 22.839406 19.171090
41 16.983279 19.818497
42 25.142082 20.335157
43 26.104740 20.560474
44 28.912188 23.826884
45 17.843957 24.998282
46 34.530743 30.764287
47 27.698383 30.802396
48 41.514822 42.821195
You can compare the predicted values with actual values.
Step 4: Evaluating Model Performance
To evaluate the model performance, the best metric is the R-squared score (Coefficient of determination). It measures the proportion of the variance in the dependent variable that is predictable from the independent variables.
from sklearn.metrics import r2_score # get the predicted values for test dat y_pred = lr_model.predict(X_poly) r2 = r2_score(y, y_pred) print(r2)
Outout
0.9321137090423877
The r2_score is the most common metric used to evaluate a regression model. The high score indicates a better fit of the model with data. 1 represent perfect fit and 0 represents no relation between the predicted values and actual values.
Result Explanation − You can examine the above metrics. Our model shows an R-squared score of around 0.932, which means that approximately 93% of data points are scattered around the fitted regression curve. Another interpretation is that 93% of the variation in the output variables is explained by the input variables.
Step 5: Visualize the polynomial regression results
Let's visualize the regression results for better understanding. We use the pyplot module from the Matplotlib library to plot the graph.
import matplotlib.pyplot as plt
# Visualize the polynomial regression results
plt.scatter(X, y, color="green")
plt.plot(X, y_pred, color='red', label=f'Polynomial Regression (degree={degree})')
plt.xlabel("Temperature (C)")
plt.ylabel("Ice Cream Sales (units)")
plt.legend()
plt.title('Polynomial Regression')
plt.show()
Output
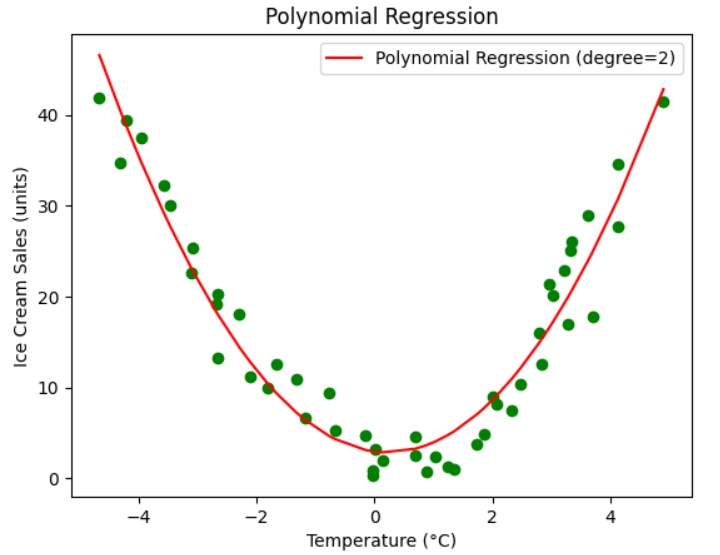
The above graph shows that the polynomial regression with degree 2 fits well with the original data. The polynomial curve (parabola), in red color, represents the best-fit regression curve. This regression curve is used to predict the value. The graph also shows that the predicted values are close to the actual values.
Step 5: Model Prediction for New Data
Up to now, we have predicted the values in the dataset. Let's use our regression model to predict new, unseen data.
Let's take the Temperature (C) as 1.9929C and predict the units of Ice Cream Sales.
# Predict a new value X_new = np.array([[1.9929]]) # Example value to predict X_new_poly = poly_features.transform(X_new) y_new_pred = lr_model.predict(X_new_poly) print(y_new_pred)
Output
[8.57450466]
The above result shows that the predicted value of Ice cream sales is 8.57450466.