Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Prove that the vertex cover is NP complete in TOC
It is the subset(minimum size) of vertices of a graph G such that every edge in G incident to at least one vertex in G.
Vertex Cover (VC) Problem
To prove VC is NP-complete we have to prove the following −
VC is Non-deterministic Polynomial (NP).
A NPC problem can be reduced into VC.
To prove VC is NP, find a verifier which is a subset of vertices which is VC and that can be verified in polynomial time. For a graph of n vertices it can be proved in O(n2). Thus, VC is NP.
Now consider the “clique” problem which is NPC and reduce it into VC to prove NPC. Clique of a graph G is a subset of vertices such that these vertices form a complete subgraph in the given graph G.
The two graphs titles (a) and (b) are given below for the VC problem −
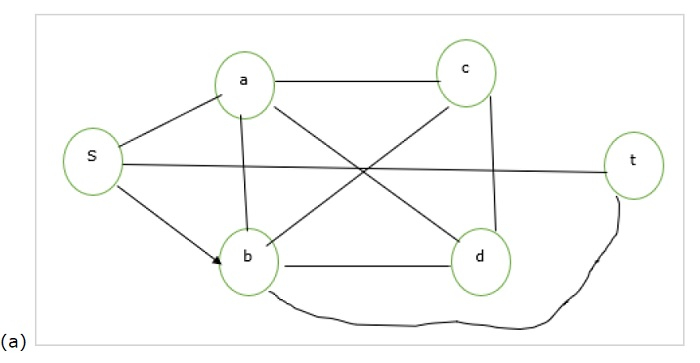
Consider graph (a), here clique is {a,b,c,d}.
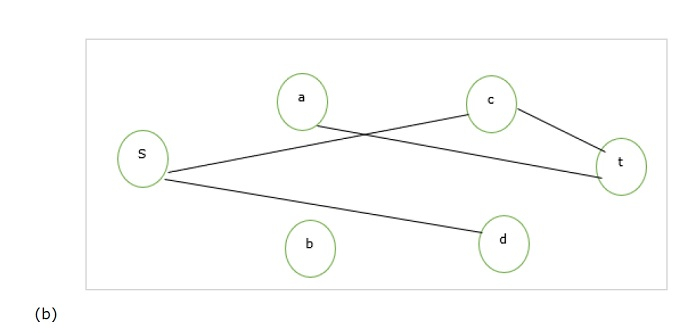
Now calculate a graph as shown in (b) which is as follows −
Completed graph of all the vertices in (a) – (a)
For the graph (b), we can say that the vertex cover is {s,t} which covers all the edges of the (b). This {s,t} = {a,b,c,d,s,t} – {Clique of (a)} Thus conversely, we can say that we can reduce clique into the VC problem and conversely can find both VC and clique of a given undirected graph. This means VC is NP-complete reducible.
Hence proved that VC is an NPC.
6K+ Views
