
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Proof that travelling salesman problem is NP Hard
The Traveling Salesman Problem (TSP) involves a salesman who must start at a given location, visit every other city exactly once, and then return to the starting point. The goal of TSP is to find the shortest path that minimizes the total distance traveled.
Travelling Salesman Problem : NP?Hard
This problem is classified as NP-hard, which indicates that it cannot be solved in polynomial time. NP-hard refers to a class of problems for which no efficient solution exists. A simple example of an NP-hard problem is the subset sum problem.
To better understand how a salesman travels to multiple cities while minimizing distance, let us consider an example that involves five cities.
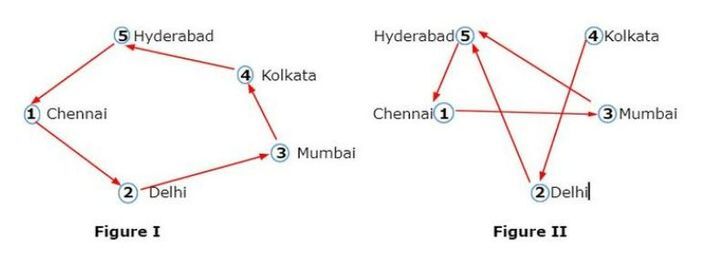
Which option would we prefer between the two figures?
In these figures, Figure II represents the shortest path. In Figure I, when the salesman travels from Chennai (point 1) to Hyderabad (point 5), he takes a longer route, covering the distance of 1 -> 2 -> 3 -> 4 -> 5 -> 1. Conversely, in Figure II, the salesman can directly reach point 3 (Mumbai), significantly reducing travel time and covering the minimum distance of 1 -> 3 -> 5 -> 1.
Can we determine the possibilities for the problem involving 32 cities?
The formula for the possibilities is given by (n-1)!/2.
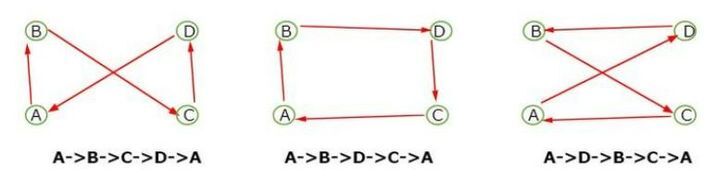
4 Cities Problem
In the case of 4 cities problem, we have a calculation like, (4-1)!/2 = 3!/2
So there is a total of 3 possibilities for covering the distance.
Let us look at the picture and understand the possibilities of 4 cities.
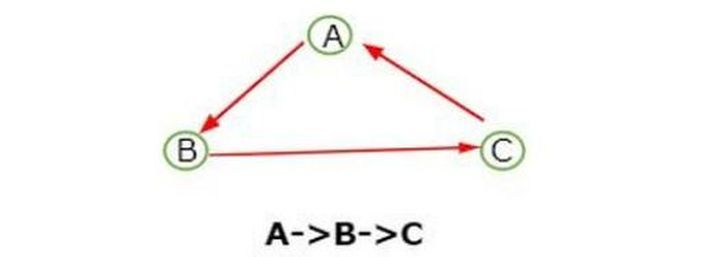
3 Cities Problem
In the case of 3 cities problem, there is only 1 possibility for covering the distance.
Now, let takes the problem of 41 cities where we can understand the NP-hard problem.
In the case of 41 cities, we will have 40!/2 solutions for a salesman to travel to each city.
If the salesman reaches each city and finds the best possible route it will take the following:
40! / (2*106) seconds Or 40! / (2*106*24*60*60) days Or 40! / 365*(2*106*24*60*60) years = 6.8 * 1013 times which is more than the life of earth.
Therefore, it is impossible to find all possible routes and get the optimal solution and this type of problem is called NP-hard.
Conclusion
We explored the concept of the traveling salesman problem, which is classified as NP-hard. We visualize various diagrams that illustrate the idea of minimizing distance and finding the best possible route. But, looking into the NP-hard nature of this problem, we realized that it cannot be solved in polynomial time. This is what makes it NP-hard.

