
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Proof that the Dominant Set of a Graph is NP-Complete
A Dominant set of a graph is NP-complete is the subset of vertices such that every vertex in the subset or adjacent vertex in the subset. The full form of NP is "Nondeterministic polynomial" which will check the problem in polynomial time and it means that we can check whether the solution is correct or not in polynomial time. The polynomial time has the best complexity to the code like the time complexity of linear search - n, Binary search - logn, Merge sort- n(log)n, etc. The NP-complete graph provides a good solution in a reasonable amount of time. This application is used in the field of network control, topology creation in the computer lab, social networking, and distributed computing.
Let us understand and check the nodes have a dominant set of graphs in NP-complete.
A vertex is said to dominate itself and each of its neighbors.
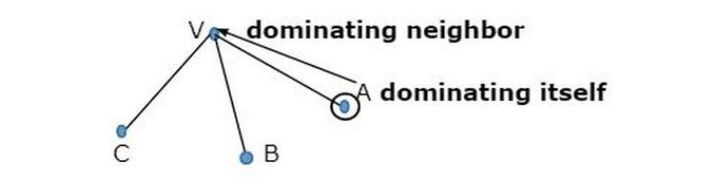

We see there are two figures which show the grey color of nodes in the graph dominating in nature.
G = V, E
Parameters
G is considered a graph, V is considered a vertex, and E is considered an edge.
Determine whether a graph has a Dominating Set of size k given a graph G(V, E) and an integer k. An input that is designated for the problem is considered an instance of the problem. A graph G (V, E) and an integer k serve as examples of the Dominating Set problem, which asks whether the graph can have a dominating set in G. Since an NP-Complete problem is by definition one that is both in NP and NP-hard, there are two components to the demonstration that a problem is NP-Complete ?
Dominating set in NP-complete
If there is an NP problem Y that is reducible to X in polynomial time, then X is NP-Complete. NP-Complete problems are just as difficult as NP problems. If a problem is part of both the NP and NP-Hard problems, it is NP-Complete. In polynomial time, a non-deterministic Turing machine can solve an NP-Complete problem. When a problem is np-complete, it has both np and np hard combined.
This means that problems with np solutions can be verified in polynomial time.
The real example of NP-complete having the dominating set such as ?
Problems with decision-making.
Graphs that are consistent.
Nondeterministic algorithm for searching
NP_search( key ) {
arraylist[100];
i = array_check(key);
if(list[i]==key) {
searching found at index i.
} else {
searching found at index i.
}
}
So, the total time complexity of this algorithm is O(1) but we don't know which search technique is more useful to solve this problem and this is said to be a nondeterministic algorithm.
Dominating set in NP-hard
If there is an NP-Complete problem Y that is reducible to X in polynomial time, then problem X is NP-Hard. NP-Hard problems are just as difficult as NP-Complete problems. An NP-Hard problem does not have to be in the NP class.
If every NP problem can be solved in polynomial time, it is said to be NP-Hard. Many times, a specific problem is used to solve and reduce other problems.
The real example of NP-hard having the dominating set such as ?
Hamiltonian cycle
optimization problem
shortest route
Conclusion
We learned the concept of a dominant set of a Graph is NP complete. We saw how discrete mathematics is an important aspect to connect these problems for example Hamilton cycle, shortest route, etc. In the programming aspect, the NP-complete is a class of problems with hard to find but straightforward-to-verify the solution in polynomial time.

