Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Pseudo-Palindromic Paths in a Binary Tree in C++
Suppose we have a binary tree where node values are digits from 1 to 9. One path in the binary tree is said to be pseudo-palindromic when at least one permutation of the node values in the path is a palindrome. We have to find the number of pseudo-palindromic paths going from the root node to leaf nodes.
So, if the input is like
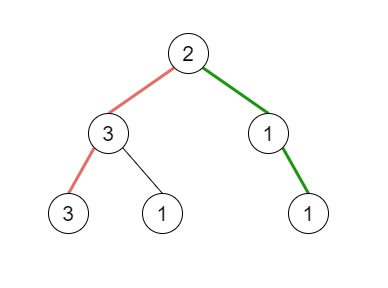
then the output will be 2, this is because there are three paths going from the root node to leaf nodes − red path follows [2,3,3], the green path follows [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged as [3,2,3] and the green path [2,1,1] can be rearranged as [1,2,1].
To solve this, we will follow these steps −
Define a function ok(), this will take an array v,
odd := 0
for each element it in v −
odd := odd + it AND 1
return true when odd is 0 OR odd is 1, otherwise false
Define a function dfs(), this will take node, array v,
if node is null, then −
return
increase v[val of node] by 1
if left of node is null and right of node is null, then −
if ok(v) is true, then −
(increase ret by 1)
decrease v[val of node] by 1
return
dfs(left of node, v)
dfs(right of node, v)
decrease v[val of node] by 1
From the main method, do the following −
ret := 0
Define an array cnt of size 10
dfs(root, cnt)
return ret
Example
Let us see the following implementation to get a better understanding −
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}
else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}
else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
class Solution {
public:
int ret;
bool ok(vector <int>& v){
int odd = 0;
for (auto& it : v) {
odd += it & 1;
}
return odd == 0 || odd == 1;
}
void dfs(TreeNode* node, vector <int>& v){
if (!node)
return;
v[node->val]++;
if (!node->left && !node->right) {
if (ok(v))
ret++;
v[node->val]--;
return;
}
dfs(node->left, v);
dfs(node->right, v);
v[node->val]--;
}
int pseudoPalindromicPaths (TreeNode* root) {
ret = 0;
vector<int> cnt(10);
dfs(root, cnt);
return ret;
}
};
main(){
Solution ob;
vector<int> v = {2,3,1,3,1,NULL,1};
TreeNode *root = make_tree(v);
cout << (ob.pseudoPalindromicPaths(root));
}Input
{2,3,1,3,1,NULL,1}Output
2
235 Views
