Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find length of longest consecutive path of a binary tree in python
Suppose we have a binary tree; we have to find the longest path in the binary tree.
So, if the input is like
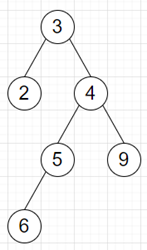
then the output will be 5 as longest consecutive sequence is [2, 3, 4, 5, 6].
To solve this, we will follow these steps −
- if root is null, then
- return 0
- maxPath := 0
- Define a function helper() . This will take node
- inc := 1, dec := 1
- if left of node is not null, then
- [left_inc, left_dec] := helper(left of node)
- otherwise,
- [left_inc, left_dec] := [0, 0]
- if right of node is not null, then
- [right_inc, right_dec] := helper(right of node)
- otherwise,
- [right_inc, right_dec] := [0, 0]
- if left of node is not null and value of node - value of left of node is same as 1, then
- inc := maximum of inc and (left_inc + 1)
- otherwise when left of node is not null and value of node - value of left of node is same as -1, then
- dec := maximum of dec and (left_dec + 1)
- if right of node is not null and value of node - value of right of node is same as 1, then
- inc := maximum of inc and (right_inc + 1)
- otherwise when right of node is not null and value of node - value of right of node is same as -1, then
- dec := maximum of dec and (right_dec + 1)
- if left of node is not null and right of node is not null and value of left of node - value of node is same as 1 and value of node - value of right of node is same as 1, then
- maxPath := maximum of maxPath and (left_dec + right_inc + 1)
- otherwise when left of node node is not null and right of node is not null and value of left of node - value of node is same as -1, then
- maxPath := maximum of maxPath and (left_inc + right_dec + 1)
- maxPath := maximum of maxPath, inc and dec
- return inc, dec
- From the main method do the following:
- helper(root)
- return maxPath
Let us see the following implementation to get better understanding −
Example
class TreeNode: def __init__(self, data, left = None, right = None): self.val = data self.left = left self.right = right def print_tree(root): if root is not None: print_tree(root.left) print(root.val, end = ', ') print_tree(root.right) class Solution: def solve(self, root): if not root: return 0 self.maxPath = 0 def helper(node): inc, dec = 1, 1 if node.left: left_inc, left_dec = helper(node.left) else: left_inc, left_dec = 0, 0 if node.right: right_inc, right_dec = helper(node.right) else: right_inc, right_dec = 0, 0 if node.left and node.val - node.left.val == 1: inc = max(inc, left_inc + 1) elif node.left and node.val - node.left.val == -1: dec = max(dec, left_dec + 1) if node.right and node.val - node.right.val == 1: inc = max(inc, right_inc + 1) elif node.right and node.val - node.right.val == -1: dec = max(dec, right_dec + 1) if (node.left and node.right and node.left.val - node.val == 1 and node.val - node.right.val == 1): self.maxPath = max(self.maxPath, left_dec + right_inc + 1) elif (node.left and node.right and node.left.val - node.val == -1 and node.val - node.right.val == -1): self.maxPath = max(self.maxPath, left_inc + right_dec + 1) self.maxPath = max(self.maxPath, inc, dec) return inc, dec helper(root) return self.maxPath ob = Solution() root = TreeNode(3) root.left = TreeNode(2) root.right = TreeNode(4) root.right.left = TreeNode(5) root.right.right = TreeNode(9) root.right.left.left = TreeNode(6) print(ob.solve(root))
Input
root = TreeNode(3) root.left = TreeNode(2) root.right = TreeNode(4) root.right.left = TreeNode(5) root.right.right = TreeNode(9) root.right.left.left = TreeNode(6)
Output
5
Updated on: 02-Dec-2020
147 Views
Advertisements