Program to check whether given graph is bipartite or not in Python

Suppose we have one undirected graph, we have to check whether the graph is bipartite or not. As we know a graph is bipartite when we can split the nodes of the graph into two sets A and B such that every edge {u,v} in the graph has one node u in A and another node v in B.

So, if the input is like

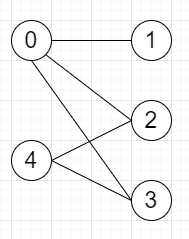
Then the output will be True, [0,4] are in set A and [1,2,3] are in set B, and all edges are from A to B or B to A, not A to A or B to B.

To solve this, we will follow these steps−

• Define a function dfs() . This will take source

• for each vertex in graph[source], do

  • if color[vertex] is not same as -1, then

    • if color[vertex] is same as color[source], then

      • result[0] := False

      • return

    • go for the next iteration

  • color[vertex] := 1 - color[source]

  • dfs(vertex)

• From the main method, do the following−

• n := size of arr

• graph := empty adjacency list for vertices 0 to n-1

• for i in range 0 to n, do

  • for each j in arr[i], do

    • insert i into graph[j]

    • insert j into graph[i]

  • color := a list of size n and fill with -1

  • result := a list with one True value

• for i in range 0 to n, do

  • if color[i] is same as -1, then

  • dfs(i)

• return result[0]

Let us see the following implementation to get better understanding −

Example

 Live Demo

from collections import defaultdict
class Solution:
   def solve(self, arr):
      n = len(arr)
      graph = [set() for i in range(n)]
      for i in range(n):
         for j in arr[i]:
            graph[j].add(i)
            graph[i].add(j)
      color = [-1] * n
      result = [True]
      def dfs(source):
      for child in graph[source]:
         if color[child] != -1:
            if color[child] == color[source]:
               result[0] = False
               return
            continue
      color[child] = 1 - color[source]
      dfs(child)
   for i in range(n):
      if color[i] == -1:
      dfs(i)
   return result[0]
ob = Solution()
graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]
print(ob.solve(graph))

Input

graph = [[1,2,3],[0],[0,4],[0,4],[2,3]]

Output

True