Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print all nodes in a binary tree having K leaves in C++
In this problem, we are given a binary tree and an integer K and we have to print all nodes of the binary tree that have K leaves in their child subtree.
The binary tree is a special tree whose each node has at max two nodes (one/two/none).
The leaf node of a binary tree is the node at end of the tree.
Let’s take an example to understand the problem −
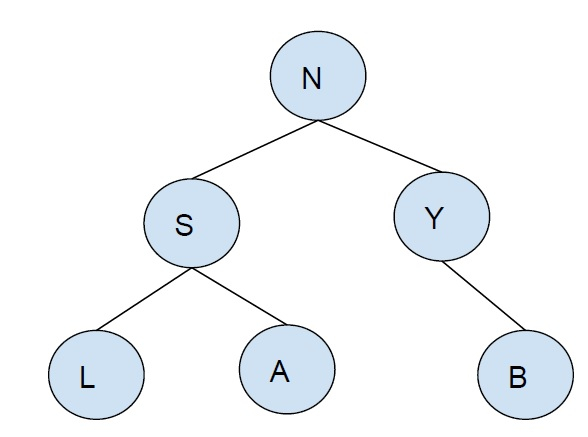
K = 2
Output − {S}
To solve this problem, we will do traversal (postorder) for the tree. Now, we will see each left subtree and right subtree if the sum of leaves is K, print current node otherwise recursively call, subtree’s leaves count.
This solution is based on traversing so complexity will be of the order of the size of the tree. Time complexity − O(n)
Example
Program to implement the above approach
#include<bits/stdc++.h>
using namespace std;
struct Node{
char data ;
struct Node * left, * right ;
};
struct Node * insertNode(char data){
struct Node * node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int nodeWithKLeave(struct Node *ptr,int k){
if (ptr == NULL)
return 0;
if (ptr->left == NULL && ptr->right == NULL)
return 1;
int total = nodeWithKLeave(ptr->left, k) + nodeWithKLeave(ptr->right, k);
if (k == total)
cout<<ptr->data<<" ";
return total;
}
int main() {
struct Node *root = insertNode('A');
root->left = insertNode('B');
root->right = insertNode('K');
root->left->left = insertNode('N');
root->left->right = insertNode('S');
root->left->left->left = insertNode('X');
root->left->left->right = insertNode('H');
root->right->right = insertNode('E');
root->right->left = insertNode('T');
root->right->left->left = insertNode('O');
root->right->left->right = insertNode('P');
int K = 2;
cout<<"Nodes with "<<K<<" leaves is :\n";
nodeWithKLeave(root, K);
return 0;
}Output
Nodes with 2 leaves are: N T
93 Views
