Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Product of given N fractions in reduced form in C
Given the numerator num and denominator den of N fractions, the task is to find the product N fractions and output should be in reduced form.
Like in the given figure below we have two fractions ”4/5” and “3/4” we have found the product of those two factions where the numerator of first is multiplied by the numerator of second and the denominator of the first is multiplying the denominator of the second. Now the final result is “12/20” which can be reduced so the output shall be “3/5 ” likewise we have to develop a program to solve the given problem.
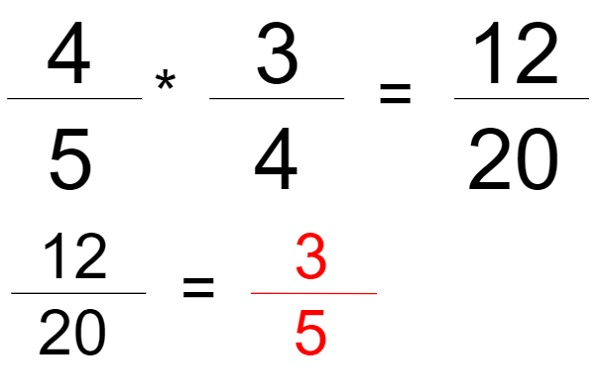
Input
fraction f[3] = {{1,2},
{2,1},
{5,6}}Output
5/6
Explanation − 1/2 * 2/1 * 5/6 = 10/12 so we can reduce it as 5/6.
Input
fraction f[2] = {{2, 3},
{1,4}}Output
1/6
Explanation − 2/3 * 1/4 = 2/12 which can be reduced as 1/6
Approach used below is as follows to solve the problem
To solve the above problem we can product all the denominators and numerators, store the result in another variables prod_den and prod_num that will be the final denominator and final numerator respectively now we have to find the reduced form, for that we have to find the GCD (greatest common divisor) of the prod_num and prod_den and divide the prod_num and prod_den with their respective GCD.
Algorithm
Start
Declare a struct fraction with following elements
1. num, 2. den
In function int GCD(int a, int b)
Step 1→ If a == 0 then,
Return b
Step 2→ Return GCD(b % a, a)
In function int product(int n, fraction f[])
Step 1→ Initialize prod_num = 1 prod_den = 1
Step 2→ Loop For i = 0; i < n; i++
prod_num = prod_num * f[i].num
prod_den = prod_den * f[i].den
Step 3→ Declare and initialize gcd = GCD(prod_num, prod_den)
Step 4→ prod_num = prod_num / gcd
Step 5→ prod_den = prod_den / gcd
Step 6→ Print prod_num, prod_den
In Function int main()
Step 1→ Declare struct fraction f[3] = {
{1,2},
{2,1},
{5,6}}
Step 2→ Declare and initialization n as sizeof(f)/sizeof(f[0])
Step 3→ product(n, f)
StopExample
#include <stdio.h>
struct fraction{
int num;
int den;
};
// Function to return gcd of a and b
int GCD(int a, int b){
if (a == 0)
return b;
return GCD(b % a, a);
}
//fucntion to print the result
int product(int n, fraction f[]){
int prod_num = 1, prod_den = 1;
// finding the product of all N
// numerators and denominators.
for (int i = 0; i < n; i++) {
prod_num *= f[i].num;
prod_den *= f[i].den;
}
// Finding GCD of new numerator and
// denominator
int gcd = GCD(prod_num, prod_den);
// finding reduced form
prod_num /= gcd;
prod_den /= gcd;
printf("%d/%d
", prod_num, prod_den);
return 0;
}
int main(){
struct fraction f[3] = {
{1,2},
{2,1},
{5,6}};
int n = sizeof(f)/sizeof(f[0]);
product(n, f);
return 0;
}Output
If run the above code it will generate the following output −
5/6
128 Views
