Polar Form of Complex Numbers

Introduction

The polar form of a complex number $\mathrm{z\:=\:x\:+\:iy\:is\:r(\cos\theta\:+\:i\:\sin\theta)}$.In mathematics, there are various coordinate systems to represent real numbers. However, the complex number system can be represented in two ways, i.e., rectangular and polar coordinate systems. In this tutorial, we will learn about complex numbers, their representation in polar form, and some basic formulae related to complex numbers with solved examples.

Complex Number

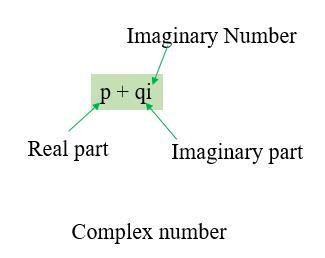
The complex number is a category of a number system associated imaginary numbers. In other words, complex numbers are the summation of real and imaginary numbers. The imaginary numbers are nothing but the square root of the negative integers. The complex number is usually represented in the form of $\mathrm{p\:+\:iq}$. In this case, p is the real part, and q is the imaginary part. In addition, i is an imaginary number, and its value is $\mathrm{\sqrt{-1}}$. Some examples of complex numbers include 5 + 6𝑖, −3𝑖, −1 + 9𝑖, etc.

Polar Form of Complex Number

In polar form, the complex number can be represented by the combination of modulus and argument. Let’s consider a complex number, i.e., $\mathrm{z\:=\:p\:+\:iq}$. The polar form of the given complex number can be written as

$$\mathrm{z\:=\:r\:(\cos\theta\:+\:i\sin\theta)}$$

where $\mathrm{r\:=\:\lvert\:z\:\rvert\:=\:\sqrt{p^{2}\:+\:q^{2}}\:=\:modulus\:of\:the\:complex\:number}$

$\mathrm{p\:=\:r\cos\theta\:,\:q\:=\:r\sin\theta}$

Hence, $\mathrm{\theta\:=\:\tan^{-1}(\frac{q}{p})\:=\:argument\:of\:the\:complex\:number}$

Representation of Polar Graphs

Let’s consider a complex number, i.e., $\mathrm{z\:=\:p\:+\:iq}$. The graphical representation of the complex number in polar form is shown in the given figure.

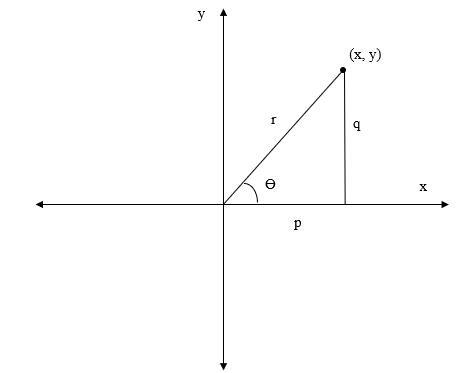
We can see that the X-axis denotes the real part, and Y-axis represents the imaginary part of the complex number. In addition, r is the length of the vector and 𝜃 is the angle made by the vector with the X-axis.

Now, using the Pythagorean theorem,

$$\mathrm{Hypotenuse^{2}\:=\:Base^{2}\:+\:Height^{2}}$$

$$\mathrm{r^{2}\:=\:P^{2}\:+\:q^{2}}$$

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{p^{2}\:+\:q^{2}}}$$

Again,$\mathrm{\cos\theta\:=\:\frac{Base}{Hypotenuse}\:=\:\frac{p}{r}}$ (∵Using trigonometric ratios)

$$\mathrm{\Longrightarrow\:p\:=\:r\cos\theta}$$

Similarly, $\mathrm{\sin\theta\:=\:\frac{Height}{Hypotenuse}\:=\:\frac{q}{r}}$(∵Using trigonometric ratios)

$$\mathrm{\Longrightarrow\:q\:=\:r\sin\theta}$$

Now, put the values of p and q in the original equation of the complex number. we get

$$\mathrm{z\:=\:p\:+\:iq\:=\:r(\cos\theta\:+\:i\sin\theta)}$$

The obtained expression is the required polar form of the complex number.

Euler Formula and De Moivre’s Theorems

Euler’s formula establishes the relationship between the complex exponentials and trigonometric functions. De Moivre’s theorem is applied to raise complex numbers to different powers. Let’s discuss both formula and theorem in detail.

Euler formula:

The Euler formula for complex numbers is $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

Let’s derive this formula.

Derivation of Euler formula −

The Taylor series expansion of $\mathrm{e^{x}}$ is

$$\mathrm{e^{x}\:=\:1\:+\:x\:+\:\frac{x^{2}}{2!}\:+\:\frac{x^{3}}{3!}\:+\:\frac{x^{4}}{4!}\:+\:.........}$$

$\mathrm{Now\:,\:put\:x\:=\:i\theta}$

Hence, $\mathrm{e^{i\theta}\:=\:1\:+\:i\theta\:+\:\frac{(i\theta)^{2}}{2!}\:+\:\frac{(i\theta)^{3}}{3!}\:+\:\frac{(i\theta)^{4}}{4!}\:+\:.........}$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:1\:+\:i\theta\:-\:\frac{\theta^{2}}{2!}\:-\:\frac{i\theta^{3}}{3!}\:+\:\frac{\theta^{4}}{4!}\:+\:.........}$$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:+\:i\:(\theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)}$$

From the Taylors series expansion,

$\mathrm{(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:=\:\cos\theta\:and\:(\theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)\:=\:\sin\theta}$

Therefore, $\mathrm{e^{i\theta}\:=\:\cos\theta\:+\:i\:\sin\theta}$ or $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

De Moivre’s theorem:

The formula related to De Moivre’s theorem is

$$\mathrm{(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$$

Derivation of De Moivre’s formula −

We will prove the above formula using the principle of mathematical induction.

Let’ consider $\mathrm{Z(m)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$

Case 1 −

Consider m = 1

$\mathrm{LHS\:=\:(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:(p(\cos\theta\:+\:i\:\sin\theta))^{1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

$\mathrm{RHS\:=\:p^{m}\:(\cos\:m\theta\:+\:i\sin\:m\theta)\:=\:p^{1}\:(\cos\:1.\theta\:+\:i\:\sin\:1.\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

Since LHS = RHS, Z (m) is true form m = 1.

Case 2 −

Suppose the above formula is true for m = n

Therefore,

$\mathrm{Z(n)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{n}\:=\:p^{n}(\cos\:n\theta\:+\:i\:\sin\:n\theta)}$

Case 3 −

Consider $\mathrm{m\:=\:n\:+\:1}$

$\mathrm{LHS\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{m}\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n\:+\:1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n}\:\times\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:p^{n}(\cos\:n\:\theta\:+\:𝑖i\:\sin\:n\theta)\:\times\:p(\cos\:\theta\:+\:i\:\sin\:\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}(\cos\:n\theta\:.\:\cos\theta\:+\:\cos\:n\theta\:.\:i\:\sin\theta\:+\:i\:\sin\:n\theta\:.\:\cos\:\theta\:+\:\sin\:n\theta\:.\:i\sin\:\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:n\theta\:.\:\cos\:\theta\:-\:\sin\:n\theta\:.\:\sin\theta)\:+\:i(\cos\:n\theta\:.\:\sin\:\theta\:+\:\sin\:n\theta\:.\:\cos\:\theta)]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:(n\theta\:+\:\theta))\:+\:i(\sin\:(n\theta\:+\:\theta))]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos(n\:+\:1)\theta)\:+\:i(\sin(n\:+\:1)\theta)]\:=\:RHS}$

Since LHS = RHS, Z (m) is true form m = n+1.

Therefore, the above statement is found to be true for all values of m.

Solved Examples

1)Evaluate the argument and modulus of the given complex number $\mathrm{2\:+\:2i}$

Answer − The given complex number is

$$\mathrm{z\:=\:2\:+\:2i}$$

The argument of the complex number is given by

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{2}{2}\:=\:\tan^{-1}\:=\:\frac{\pi}{4}}$$

The modulus of the complex number is given by

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{2^{2}\:+\:2^{2}}\:=\:\sqrt{8}\:=\:2\sqrt{2}}$$

∴ The argument and modulus of the complex number are found to be $\mathrm{\frac{\pi}{4}\:and\:2\sqrt{2}}$

2) Express $\mathrm{7e^{3i}}$ in the rectangular form (p + iq) of a complex number using Euler’s formula.

Answer − Using Euler’s formula,

$$\mathrm{e^{i\theta}\:=\:\cos\:\theta\:+\:i\sin\:\theta}$$

Here,$\mathrm{\theta\:=\:3}$

Hence, $\mathrm{e^{3i}\:=\:\cos\:3\:+\:i\sin\:3\:=\:-0.99\:+\:i(0.14)}$

$$\mathrm{7e^{3i}\:=\:7(-0.99\:+\:i(0.14))\:=\:-6.93\:+\:0.98i}$$

Therefore,$\mathrm{7\:e^{3i}\:=\:-6.93\:+\:0.98i}$

3)Determine the value of the given complex number using De Moivre’s formula: $\mathrm{(\sqrt{3}\:+\:i)^{6}}$

Answer − The given complex number is $\mathrm{\sqrt{3}\:+\:i}$

We have to convert the given complex number into its polar form.

The argument of the complex number is given by

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{1}{\sqrt{3}}\:=\:\frac{\pi}{6}}$$

The modulus of the complex number is given by

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{(\sqrt{3})^{2}\:+\:1^{2}}\:=\:\sqrt{4}\:=\:2}$$

The polar form of the complex number is $\mathrm{\sqrt{3}\:+\:i\:=\:2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})}$

Now, $\mathrm{(\sqrt{3}\:+\:i)^{6}\:=\:[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}}$

Using the De Moivre’s formula,

$$\mathrm{[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}\:=\:2^{6}\:(\cos\:\frac{\pi}{6}\:\times\:6\:+\:i\:\sin\:\frac{\pi}{6}\times\:6)}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2^{6}\:(\cos\:\pi\:+\:i\sin\:\pi)\:=\:64\:(-1\:+\:i\:.\:0)\:=\:-64}$$

Therefore the value of $\mathrm{(\sqrt{3}\:+\:i)^{6}\:is\:-64}$

Conclusion

The present tutorial gives a brief introduction to the complex number and its polar representation. The basic definition of the complex number and its representation in polar form have been explained in this tutorial. In addition, two important formulae related to the complex number, such as Euler’s and De Moivre’s formulae, have been illustrated. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding the basic concept of the polar form of complex numbers.

FAQs

1. What are the applications of Euler’s formula?

Euler’s formula is widely used to determine the relationship between the edge and vertices of a polyhedra and trace the unit circle.

2. Can we apply De Movire’s theorem to a complex number, which is in rectangular form?

Yes. However, the complex number should be converted to its polar form first. Then, we can determine its value using De Moivre’s formula.

3. What is the range of principal arguments of a complex number?

The range of principal arguments varies from $\mathrm{-\pi\:to\:\pi}$ . That means $\mathrm{-\pi\:<\:\theta\:\leq\:\pi}$

4. What are the applications of complex numbers?

The complex numbers are extensively used in electric circuit analysis, signal processing, quantum mechanics, etc.

5. Can the modulus of a complex number be negative?

No. The modulus of a complex number is the magnitude of the vector. Hence, the magnitude is always a positive integer.