Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Complex numbers operations in Arduino
The Complex library by RobTillart helps perform complex number math in Arduino. In order to install this library, you can search for 'Complex' in library manager. The library can be found on GitHub. (Pay attention to the Readme. The library doesn't compile for Due and Teensy 3.5. A solution is provided there).
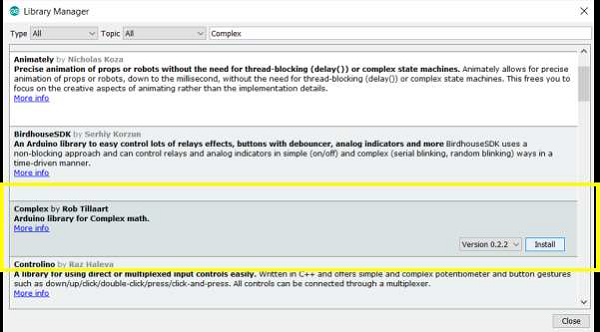
Once installed, go to: File → Examples → Complex and open the complex.ino example.
This example covers all the operations that you can perform with complex numbers. While the example is too large to reproduce here, here are a few points to note −
Complex numbers are defined as Complex var(real, imag). For example -Complex c1(10.0, -2.0);
The real part can be accessed using c1.real(). Similarly, the imaginary part can be
accessed using c1.imag().You can set real and imaginary parts of an existing complex number using
.set(real,imag). Example - c3.set(0,0).Equality operations == and != work for complex numbers. Both real and imaginary parts should match for the numbers to be equal.
Negation (c = -c) applies to both real and imaginary parts. So, (10-2i) becomes (-10+2i).
Addition and subtraction works for real and imaginary parts separately. So, (10-2i) + (3+0i) gives (13-2i)
Multiplication and division of complex numbers follows the complex algebra rules.
The modulus, or the magnitude of a complex number can be obtained using .modulus() and the phase using .phase().
The value of a complex number can be set using magnitude (m) and phase (p) using .polar(m,p)
Conjugate (negative imaginary part) and reciprocal (1/c1) of a complex number can be obtained using .conjugate() and .reciprocal().
Several other mathematical operations like power, square, sqrt, log10, etc. can be performed using the corresponding functions.
Similarly, trigonometric expressions and hyperbolic expressions of complex numbers are also calculated using the corresponding functions.
647 Views
