Complex Numbers

Introduction

• Complex numbers make it simpler to find the square root of negative values.

• The concept of complex numbers was first presented when Hero of Alexandria, a Greek mathematician, attempted to compute the square root of a negative number in the first century.

• However, he made the integers' negative values positive and got their root values.

• Additionally, the identity of complex numbers was established when the third- and second-order polynomials' negative roots were discovered by the Italian mathematician Gerolamo Cardano in the sixteenth century.

• Numerous scientific research, including those involving signal processing, electromagnetism, fluid physics, quantum mechanics, and vibration analysis, have made use of complex numbers.

• Here we will understand complex number definitions, terms, visualizations, properties, and complex number operations. In this tutorial, we will discuss complex numbers.

Definition

Real and imaginary numbers are combined to form complex numbers. The format for complex numbers is $\mathrm{a\:+\:ib}$. where $\mathrm{ib}$ is imaginary part and a is the real part.

Therefore, a complex number is a simple expression of the addition of two numbers, real and imaginary numbers. a is purely real and b is purely imaginary.

• Real numbers − All numbers that exist in the notation of the number system, such as positive, negative, zero, whole, rational, irrational, and fractional, are real numbers.

• Imaginary numbers − The numbers that are not real are imaginary. Square the imaginary number to get a negative result it is represented as $\mathrm{i\:=\:\sqrt{-1}}$

Imaginary Number iota

• Iota is an imaginary unit represented by i, and the value of iota is $\mathrm{\sqrt{-1}}$ or $\mathrm{i\:=\:\sqrt{-1}}$

• Iota is a greek letter that is widely used in mathematics to denote the imaginary part of a complex number.

• You may have encountered a situation where the discriminant is negative when solving a quadratic equation.

• For example, the quadratic equation 𝑥2 + 𝑥 + 1 = 0. Solving this using a quadratic equation results in a negative discriminant (the inner part of the square root).

Polar Forms

• The polar form of complex numbers represents complex numbers in a different way than the rectangular form.

• Complex numbers are a combination of real and imaginary numbers.

• The format for complex numbers is $\mathrm{a\:+\:ib}$.

• where ib is imaginary part and a is the real part.

• However, the complex numbers are represented as a mix of modules and arguments in polar form.

• The absolute value (modulus) is another name for a complex number's modulus. The coordinate system's real and imaginary (hypothetical) polar coordinates are used to express this polar form.

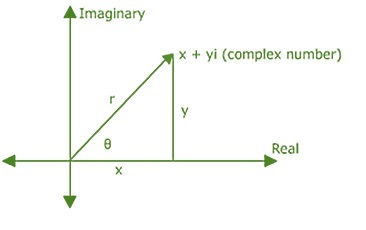
• Here, the vertical axis represents the hypothetical (imaginary) axis while the horizontal axis represents the real axis.

• Calculations are made for r and to determine the real and complex components of the coordinates. r is the vector's length, and 𝜽 is the angle that makes with the real axis.

$$\mathrm{z\:=\:x\:+\:iy}$$

$$\mathrm{z\:=\:r(\cos\theta\:+\:i\:\sin\theta)}$$

For complex numbers, r means absolute or modulus, the angle θ is known as a complex argument and $\mathrm{r\:=\:\lvert\:Z\:\rvert\:=\:\sqrt{x^{2}\:+\:y^{2}}}$

Euler's formula and De Moivre's theorem

Euler's formula describes the relationship between complex exponential functions and trigonometric functions.

Euler's Law states: For any real value of x, $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\:sin\:x}$

$$\mathrm{z\:=r\:(\:\cos\:x\:+\:i\:sin\:x)}$$

$$\mathrm{z\:=r\:e^{ix}}$$

Where i = imaginary unit, and x = angle in radians

De Moivre's Theorem is also the theorem used for complex numbers. This theorem is used to raise complex numbers to various powers.

$$\mathrm{r\:(\cos\:x\:+\:i\sin\:x)^{n}}$$

$$\mathrm{r\:(e^{ix})^{n}}$$

$$\mathrm{=\:r\:e^{ix}}$$

Therefore,

$$\mathrm{z^{n}\:=\:re^{inx}\:=\:r\:(cos\:nx\:+\:i\:sin nx)}$$

Square root of Complex numbers in algebraic form

The square root of a complex number is another complex number , whose square is a given complex number. For example, if the square root of complex number

$\mathrm{a\:+\:ib}$ is $\mathrm{\sqrt{a\:+\:ib}\:=\:x\:+\:iy}$

On squaring both sides we get,

$$\mathrm{a\:+\:ib\:=\:(x\:+\:iy)^{2}}$$

$$\mathrm{a\:+\:ib\:=\:x^{2}\:+\:(iy)^{2}\:+\:i2xy}$$

$$\mathrm{a\:+\:ib\:=\:x^{2}\:-\:y^{2}\:+\:i2xy}$$

Now compare real and imaginary parts

$\mathrm{a\:=\:x^{2}\:-\:y^{2}}$ and $\mathrm{b\:=\:2xy}$

We know that,

$$\mathrm{(x^{2}\:+\:y^{2})^{2}\:=\:(x^{2}\:-\:y^{2})^{2}\:+\:(2xy)^{2}}$$

Now put their values

$$\mathrm{(x^{2}\:+\:y^{2})^{2}\:=\:(a)^{2}\:+\:(b)^{2}}$$

$\mathrm{x^{2}\:+\:y^{2}\:=\:\sqrt{(a)^{2}\:+\:b^{2}}}$ and $\mathrm{a\:=\:x^{2}\:-\:y^{2}}$

By solving these equations, we get

$\mathrm{x\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:+\:a}\:)}{2}}\:and\:y\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:−\:a}\:)}{2}}}$

Since 𝑏 = 2𝑥𝑦 so

𝑏 > 0 if both x and y have the same sign.

𝑏 < 0 if both x and y have opposite signs.

Therefore, the square root of the complex number 𝑎 + 𝑖𝑏 is given by

$$\mathrm{\sqrt{a\:+\:ib}\:=\:x\:+\:iy}$$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:+\:a}\:)}{2}}\:\pm\:\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{(\sqrt{(a)^{2}\:+\:(b)^{2}\:−\:a}\:)}{2}}}$$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{\lvert\:z\:\rvert\:+\:a}{2}}\pm\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{\lvert\:z\:\rvert\:-\:a}{2})}}$$

Solved Examples

Example 1 − Find the modulus of complex number $\mathrm{z\:+\:1\:+\:2i}$

Solution: Given complex number is $\mathrm{z\:+\:1\:+\:2i}$ we have to find a modulus that is

$\mathrm{\lvert\:z\rvert\:=\:\sqrt{(1)^{2}\:+\:(2)^{2}}}$

$\mathrm{\lvert\:z\rvert\:=\:\sqrt{5}}$

Example 2 − Simplify the complex number $\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}}$

Solution − Given complex number is $\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}}$

Now multiply by its conjugate in the numerator as well as denominator

$$\mathrm{z\:=\:\frac{3\:+\:4i}{\sqrt2\:+\:i}\times\:\frac{\sqrt2\:-\:i}{\sqrt2\:-\:i}}$$

$$\mathrm{z\:=\:\frac{3\sqrt2\:+\:4\sqrt2i\:-\:3i\:+\:4}{2\:-\:1}}$$

$$\mathrm{z\:=\:{(3\sqrt2\:+\:4)\:+\:i(4\sqrt{2}\:-\:3)}}$$

Example 3 − Find the square of the complex number $\mathrm{z\:=\:4\:+\:3i}$

Solution − Given complex number is $\mathrm{z\:=\:4\:+\:3i}$

$$\mathrm{\lvert\:z\:\rvert\:=\:\sqrt{(4)^{2}\:+\:(3)^{2}}}$$

$$\mathrm{\lvert\:z\:\rvert\:=\:\sqrt{25}}$$

$\mathrm{\lvert\:z\:\rvert\:=\:5}$

and $\mathrm{a\:=\:4}$, $\mathrm{b\:=\:3}$

Now use the formula for the square root of the complex number

$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{\lvert\:z\:\rvert\:+\:a}{2}}\pm\frac{ib}{\lvert\:b\:\rvert}\sqrt{\frac{\lvert\:z\:\rvert\:-\:a}{2})}}$

Now put the value

$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\sqrt{\frac{5\:+\:4}{2}}\pm\frac{i3}{\lvert\:3\:\rvert}\sqrt{\frac{5\:-\:3}{2})}}$

$$\mathrm{\sqrt{a\:+\:ib}\:=\:\pm\:(\frac{9}{2}\:+\:i)}$$

Conclusion

Complex numbers are created by adding imaginary and real numbers together. A complex number normally has the form $\mathrm{a\:+\:ib}$ and is represented by the symbol z. Re(z) is utilised to represent the value "a" as the real component in this instance because both a and b are real integers, Im(z) is used to represent the value "b" as the imaginary part, and ib are also referred to as an imaginary number.

FAQs

1. What do you mean by complex numbers?

Real and imaginary numbers are combined to form complex numbers. The format for complex numbers is 𝑎 + 𝑖𝑏. where ib is imaginary part and a is the real part.

2. What is iota in complex numbers?

Iota is an imaginary unit represented by i, and the value of iota is $\mathrm{\sqrt-1}$ or $\mathrm{i\:=\sqrt-1}$

3. What do you mean by polar form of complex numbers?

In contrast to the rectangular form, complex numbers are represented differently in the polar form. Complex numbers are usually expressed in the form $\mathrm{z\:=\:x\:+\:iy}$

4. What is Euler's formula?

Euler's formula describes the relationship between complex exponential functions and trigonometric functions.

$\mathrm{z\:=\:r(\cos\theta\:+\:i\:sinx)}$

$\mathrm{z\:=\:r\:e^{ix}}$

5. What is the modulus in complex numbers?

The separation (distance) of the complex number from the origin in the Argand plane is known as the modulus of the complex number $\mathrm{z\:=\:a\:+\:ib}$ It is denoted by the symbol $\mathrm{\lvert\:z\:\rvert}$ and equals $\mathrm{z\:=\:\sqrt{(a)^{2}\:+\:(b)^{2}}}$The magnitude of the vector that represents a complex number as a vector in the Argand plane is the complex number's absolute value.