Poisson's Ratio

Introduction

Poisson's ratio is a very important material property that gives us details about how various materials can deform under fill up. Now let's take an example of the rubber band. If you take a rubber band and stretch it along its length direction, its length increases but you see at the same time in the middle the band will get thinner. So, in this regard Poisson ratio can tell us how much thinner the rubber band is going to end.

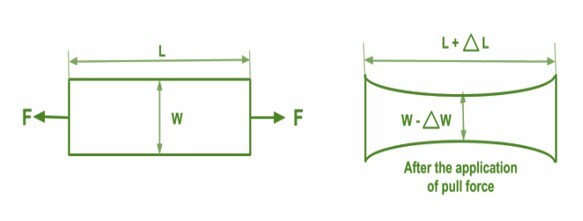
From the above figure, L is the original length of the band, but after stretch or application of force, length is changed into L+ΔL and width W is changed into W+ΔW. So, the thickness of the band becomes thinner.

What is Poisson's ratio?

Poisson’s ratio is named after the famous french mathematician named Siméon Denis Poisson who formally explained the main ratio which was published in 1827.

Now take a cuboid and if we apply a compressive force on it, it will expand in the directions which are perpendicular to the direction in which we are applying the load. We can define the Poisson's ratio as shown in the below diagram −

$$\mathrm{ \varepsilon =\frac{Lateral\: Strain}{Longitudinal\: Strain}}$$

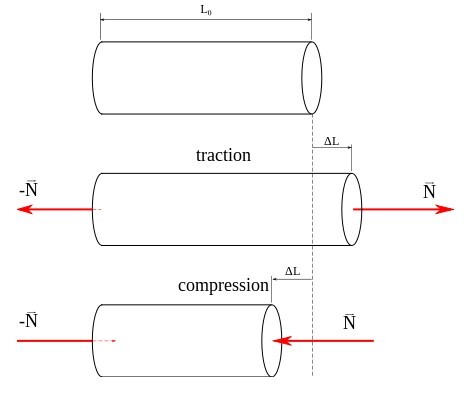
Cdang, Traction compression deformation sans poisson, CC BY-SA 3.0

We can call the direction through which the burden is exerted the longitudinal or x-axis direction which is on the x-axis, and we call the perpendicular directions the lateral directions which are on the y-axis. Now if we reverse the direction of the force to apply a tensile load, the cuboid will extend in the longitudinal direction, and it will contract in the lateral direction that is on the y-axis. The main abstraction here is that when you apply a load to a material in a direction, the material deforms in the direction of lateral.

Poisson ratio for geometric changes-

To define Poisson's ratio more precisely, let's take a closer look at the given figure, where the tensile force is applied. Firstly, we give some names to the various parameters involved here. Let the lengths can be taken as L_x, L_y and L_z are the initial dimensions of the shape cuboidal we take along the x, y, and z axes. Now, $\mathrm{\Delta L_x,\:\Delta L_y \:and\:\Delta L_z }$ are the changes that take place in these dimensions after the load has been applied. Also, changes in dimension occur on both sides of the object.

Now the strains in all three directions can be written as −

$$\mathrm{\varepsilon_x=-\frac{\Delta L_x}{L_x}\varepsilon_y=-\frac{\Delta L_y}{L_y}\varepsilon_z =-\frac{\Delta L_z}{L_z}}$$

$$\mathrm{where\:\:\varepsilon=\frac{Change\: in\: length}{Original\: length}}$$

As we know,

$$\mathrm{Poisson's\: ratio,ν=\frac {Lateral\: Strain\: or\: transverse\: strain }{Longitudinal\: Strain\: or\: axial\: strain}}$$

$$\mathrm{Poisson's\: ratio,ν=\frac{-ε_{lateral}}{ε_{longitudinal}}}$$

The minus sign here is that by convention tensile strains are positive and compressive strains are negative. As the negative of the sign in there means that since the lateral strains, it is the opposite with sign to that of the term longitudinal strains so that we get an increased Poisson's ratio.

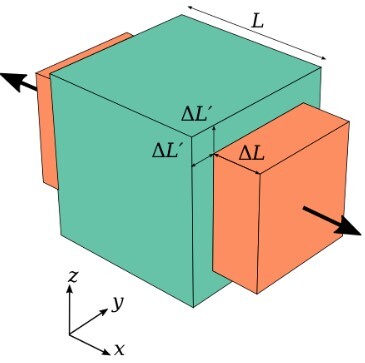
PAR, PoissonRatio, marked as public domain, more details on Wikimedia Commons

Applications

• When the liquid inner a pipe is extremely pressurized, it exerts a force inside the pipe. This resulted in stress on the material of the pipe. Due to Poisson's effect, this stress causes the pipe as it increases in length and moderately decreases in length. This can affect the pipe joints particularly. As a result, it will assemble at each section of the pipe that is joined in series.

• The rock in the earth’s crust expands or contracts in the vertical direction as a result of the applied force exerted or stress and thus deforms in the x-axis resulting in Poisson's ratio.

• Cork has a Poisson's ratio is 0. So, it contains advantages. As the cork is positioned in the bottle, the upper part of the bottle does not expand in length as it experiences a compress. If the stopper is made up of rubber material, then there would be a large extra force required to conquer the expansion of the upper part when there is rubber stopper.

Conclusion

The mentioned equation and the concepts we are going to detail only apply to isotropic materials which are the materials that have the same properties in all directions. The ratio given by the Poisson of materials that are stable, isotropic and linear that is elastic must be considered to be in between the range of −1.0 and +0.5. But otherwise, the value for Poisson’s ratio is normal, it lies between the range of 0.0 and 0.5.

The table shows some of Poisson’s ratios of common substances −

Material	Poisson's Ratio
Copper	0.33
Concrete	0.2
Rubber	0.49

Material	Poisson's Ratio
Cork	0
Glass	0.18 - 0.3
Gold	0.43
Limestone	0.2 - 0.3

FAQs

1. What will be the value of Poisson’s ratio in the metal steel?

Normally Poisson's ratio in the metal steel is between 0.27 value to 0.30 value.

2. The longitudinal strain of a wire is given by 0.25 and the worth of the Poisson ratio of the wire is 0.5. Calculate lateral strain generated in the given wire.

$$\mathrm{Given:\: Strain\: along\: the\: longitudinal\: direction\: of\: the\: wire,\: \varepsilon_{longitudinal} = 0.25}$$

The Poisson ratio of the given wire = 0.5

As we know for Poisson's ratio −

$$\mathrm{ ν= \frac{Lateral\: Strain }{Longitudinal\: Strain}\:or\:ν=\frac{\varepsilon_{lateral}}{\varepsilon_{longitudinal}} }$$

$$\mathrm{0.5=\frac{-Lateral strain}{0.25} }$$

$$\mathrm{Lateral \:Strain\: = 0.125}$$

Therefore, the lateral strain in the wire will be 0.125.

3. For a metal, what will be the maximum and minimum value for Poisson's ratio?

The standard of Poisson's ratio for a metal lies between points 0 to 0.5. The value is to be positive this is for the reason that if we applied the force that is in strain along a longitudinal direction then the strain along the lateral direction will decrease for the materials.

4. Is the worth of Poisson's ratio more substantial than 1 possible?

Yes. In a certain direction, anisotropic materials have the Poisson’s ratio will be larger than 1.

5. A steel bar that length is 50 mm and its width is 25 mm. After applying a force of 25 N, the steel bar length is considerably increased by 52 mm. Calculate the change in the width.

Given: Length of the steel bar, L - 50 mm

Width of the steel bar, W - 25 mm.

$$\mathrm{The\: change \:in\: width\: is \:written\: as \:\Delta W.}$$

As we know Poisson's ratio of steel is equal to 0.3.

Longitudinal Strain,

$$\mathrm{\varepsilon_{longitudinal}=\frac {\Delta L_x}{L_x}=\frac{52-50}{50}=0.04 }$$

As we know,

$$\mathrm{ ν=\frac{Lateral\: Strain }{Longitudinal\: Strain }}$$

$$\mathrm{0.3=\frac{\frac{dW}{25}}{0.04}}$$

$$\mathrm{dW=0.012×0.04×25}$$

$$\mathrm{dW=0.3 mm}$$

Therefore, the width of the steel bar will be reduced to 0.3 mm.

6.A wire stretched of length 5 m of length to 0.5 cm. Calculate the lateral strain that is produced in the wire. (Poison’s ratio of wire, ν = 0.26)

Given: Length, L = 5m

$$\mathrm{Change\: in\: length\:,\Delta L=0.5 cm=5×10^{-3} m}$$

Longitudinal Strain,

$$\mathrm{Poisson's\: Ratio=\frac{Lateral \:Strain }{Longitudinal \:Strain}}$$

$$\mathrm{Lateral \:Strain=Longitudinal \:Strain×Poisson's\: ratio}$$

$$\mathrm{Lateral \:Strain=10^{-3}×0.26}$$

$$\mathrm{Lateral \:Strain=2.6×10^{-4}}$$