Path Sum IV in C++

Suppose we have a list of integers that is representing a binary tree with a depth smaller than 5. If the depth of a tree is less than 5, then this tree can be represented by a list of three-digit integers. For each integer in this list −

• The hundreds digit is representing the depth D of this node, 1 <= D <= 4.

• The tens digit is representing the position P of this node in the level it belongs in the range, 1 to 8. The position is the same as that in a full binary tree.

• The units digit is used to represent the value V of this node, 0 <= V <= 9.

We have to find the sum of all paths from the root towards the leaves.

So, if the input is like [113, 215, 221], then the output will be 12, The tree that the list represents is

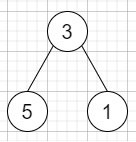
The path sum is (3 + 5) + (3 + 1) = 12.

To solve this, we will follow these steps −

• Define one map graph

• Define a function dfs(), this will take node, level, pos, sum initialize it with 0,

• isLeaf := true

• for initialize i := 0, when i < size of graph[level + 1], update (increase i by 1), do −

  • Define one pair temp := graph[level + 1, i]

  • if temp.first / 2 is same as pos, then −

    • isLeaf := false

    • dfs(temp.second, level + 1, temp.first, sum + node)

• if isLeaf is non-zero, then −

  • ret := ret + (sum + node)

• From the main method do the following,

• ret := 0

• for initialize i := 0, when i < size of nums, update (increase i by 1), do −

  • x := nums[i]

  • val := x mod 10

  • x := x / 10

  • pos := x mod 10

  • x := x / 10

  • level := x

  • insert { (shift 1 left side (level - 1) times), val } at the end of graph[level]

• dfs(graph[1, 0].second, 1, graph[1, 0].first)

• return ret

Example

Let us see the following implementation to get better understanding −

 Live Demo

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int ret;
   map <int, vector < pair <int, int> > > graph;
   void dfs(int node, int level, int pos, int sum = 0){
      bool isLeaf = true;
      for (int i = 0; i < graph[level + 1].size(); i++) {
         pair<int, int> temp = graph[level + 1][i];
         if (temp.first / 2 == pos) {
            isLeaf = false;
            dfs(temp.second, level + 1, temp.first, sum + node);
         }
      }
      if (isLeaf) {
         ret += (sum + node);
      }
   }
   int pathSum(vector<int>& nums) {
      ret = 0;
      for (int i = 0; i < nums.size(); i++) {
         int x = nums[i];
         int val = x % 10;
         x /= 10;
         int pos = x % 10;
         x /= 10;
         int level = x;
         graph[level].push_back({ (1 << (level - 1)) + pos - 1, val });
      }
      dfs(graph[1][0].second, 1, graph[1][0].first);
      return ret;
   }
};
main(){
   Solution ob;
   vector<int> v = {113,215,221};
   cout<<(ob.pathSum(v));
}

Input

{113,215,221}

Output

12